The Hough Transform is a global method for finding straight lines hidden in larger amounts of other data. It is an important technique in image processing. For detecting lines in images, the image is first binarised using some form of thresholding and then the positive instances catalogued in an examples dataset.
To understand the Hough Transform, it is important to know what the Hough space is. Each point (d,T) in Hough space corresponds to a line at angle T and distance d from the origin in the original data space. The value of a function in Hough space gives the point density along a line in the data space. The Hough Transform utilises this by the following method.
For each point in the original space consider all the lines which go through that point at a particular discrete set of angles, chosen a priori. For each angle T, calculate the distance to the line through the point at that angle and discretise that distance using an a priori chosen discretisation, giving value d.
Make a corresponding discretisation of the Hough space - this will result in a set of boxes in Hough space. These boxes are called the Hough accumulators. For each line we consider above, we increment a count (initialised at zero) in the Hough accumulator at point (d,T). After considering all the lines through all the points, a Hough accumulator with a high value will probably correspond to a line of points. In fact for uniformly distributed points, each Hough box should have a Poisson distributed count with mean given by the length of the line times discretisation width times uniform point density. Some Hough boxes will correspond to longer lines than other, resulting in the pattern seen in the star/galaxy data transform below. A count which is in the tail of the relevant Poisson distribution is unlikely to be the result of the underlying uniform data, and hence more likely to be the result of some line of points. Giving some prior model for the number of points in a line will allow a proper Bayesian assessment of whether there is a line at the relevant angle and distance from the origin.
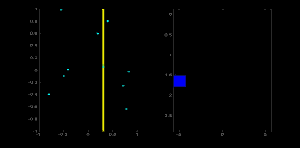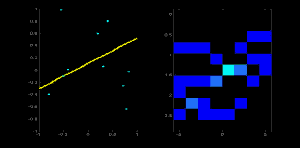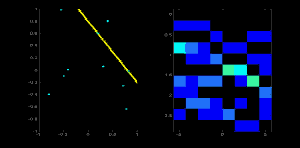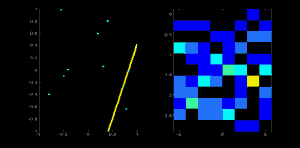To demonstrate the Hough transform we illustrate a simple problem where we can work through each point and each angle. This is shown in this movie. The data is given on the left. The result of the Hough transform is a bright orange box on the right of the figure (the Hough space) which is the result of a large number of counts for that accumulator. This box corresponds to the line of five points on the right.
The application of the Hough transform to star and galaxy data (Supercosmos Sky Survey plate UKJ005) including two major satellite tracks is shown in the figure below. The two points circled have higher than expected counts and correspond to the two main satellite tracks on the plate. The tracks are illustrated in the flythrough flythroughnew3c0.avi, (384x384) size 36MB.
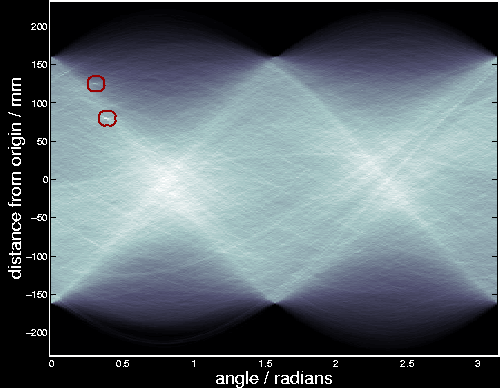
Note: assuming Poisson distributions for all the Hough accumulators ignores the dependence between accumulators at different angles. Though this independence assumption is not strictly correct, it is unlikely to have any practical effect in most circumstances. However, where curved lines appear in the data, it might be appropriate to take this dependence into account.
There are many improvements to the Hough transform, but few are able to find short line features in very noisy data. I have been working on an approach, coined Renewal Strings, which is able to do this accurately. Some illustrations of the method can be found on the Satellite Track Detection page, and two papers describing the method are available on the publications page.
