Evaluating the Invocation Process

The properties that we would like invocation to have are:

1. Correct models are always invoked, and in the correct context.
2. No matter how large the model base, the only false hypotheses invoked are those that are "similar" to the true ones.

This section presents the evidence that the proposed theory has these properties. In evaluating this theory, it is hard to apply general mathematical or computational analysis as:

1. The performance depends on the particular network used, and there are few constraints on this.
2. The network executes a complicated, non-linear computation.
3. No valid statistics are available for the performance of structure description (Chapter 6) on general position, unobscured structures.
4. It is not possible to characterize the scenes sufficiently well to predict typical structure occlusions.
5. Little information is available to assess performance of the structure description on partially obscured structures.

Three minor analytic results have been found:

(1) If all property, subcomponent, description and superclass evidence is perfect, then the correct model is always invoked. This is equivalent to saying that the object has the correct identity and all properties are measured correctly. If we then assume the worst (i.e. that the other four evidence types are totally contradictory) then evidence integration gives:

Let:
	$evd_{prop} = 1.0, evd_{subcl} = -1.0, evd_{supcl} = 1.0, evd_{subc} = 1.0,$
	$evd_{supc} = -1.0, evd_{desc} = 1.0, evd_{ass} = -1.0, evd_{inh} = 1.0$
be the eight evidence values
Then, following the integration computation:
	$v_{1} = harmmean(\{(evd_{prop},w_{prop}),(evd_{desc},w_{desc}),$ $(evd_{subc},w_{subc})\}) = 1.0$
	$v_{2} = v_{1} = 1.0$
	$v_{3} = v_{2} = 1.0$
	$v_{4} = v_{3} + c_{supcl}*evd_{supcl} = 1.0 + 0.1*1.0 = 1.1$
	$v_{5} = v_{4} + c_{inh}*evd_{inh} = 1.1 + (-0.25) * 1.0 = 0.85$
and the integrated plausibility value $p$ is:
	$p = min(max(v_{5},evd_{subcl},-1.0),1.0) = 0.85$

(2) Assume $N$ independent properties are measured as property evidence for a structure, and all are equally weighted. Then, the probability that the property evidence evaluation is greater than zero is shown in Figure 8.13, assuming all constraint ranges have the widths shown, and the data values are normally distributed. The point is to estimate how many properties are needed and what the constraint ranges on a property should be, to ensure that the property evidence almost always supports the correct identity. The graph shows that if at least 5 gaussian distributed properties are used, each with constraint width of at least 1.6 standard deviations, then there is a probability of 0.98 for positive property evidence. These results were found by simulation.

Figure 8.13: Probability of Positive Property Evidence Versus Number of Properties

(3) There is some relative ranking between the same model in different contexts: model $M_i$ has better evidence in context $C_a$ than in context $C_b$ if, and only if $p(M_i,C_a) > p(M_i,C_b)$. Further, if model $M_i$ implies model $M_j$ (i.e. a superclass), then in the same context $C$:

$$p(M_j,C) \geq p(M_i,C)$$

Unfortunately, not much can be said regarding the ranking of different models in the same context, because each has different evidence requirements.

The theory proposed in this chapter accounts for and integrates many of the major visual relationship types. The surface cluster contexts focus attention to ASSEMBLY identities (and surface contexts to SURFACE identities), the object types denote natural conceptual categories, and the different relationship links structure the paths of evidence flow. The mathematical results suggest that "correct models are always invoked" if the data is well-behaved.

The "no false invocations" requirement is not easily assessed without a formal definition of "similar", and none has been found that ensures that false invocations are unlikely. So, a performance demonstration is presented, using the model base partly shown in Appendix A with the test image, and show that the invocation process was effective and robust.

Suppose interest is in the plausibility of the trash can outer surface ("tcanoutf") as an explanation for region 9 (see Figure 3.10). The description process produces the following results:

$$\vbox{\hskip 0.5in \begin{tabular}{ll} DESCRIPTION& VALUES\\... ... boundary curvature &0.058, 0.0, 0.085, 0.0\\ \end{tabular}}$$

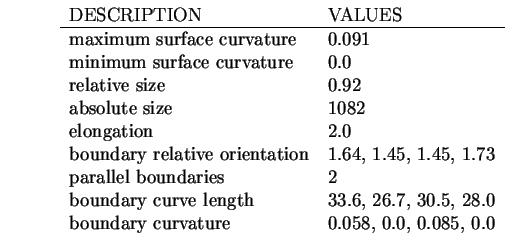
The property evidence computation is then performed, based on the following evidence constraint (all other properties are in the description "tcanfac"):

$$\vbox{\hskip 0.5in \begin{tabular}{lcccc} PROPERTY&LOW&PEAK&H... ...e maximum curvature & 0.058&0.078&0.098 &0.5\\ \end{tabular}}$$

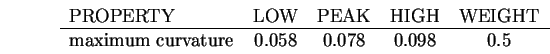
This results in a property evidence value of 0.74 with weight 0.5. After invocation converges, there are also the relationship evidence values. No subclasses, superclasses, subcomponents or associations were defined for this model, so their evidence contribution is not included. The model has a description "tcanfac" that shares properties of the trash can inner surface ("tcaninf") except for its convexity or concavity, and its evidence value is 0.66 with a weight of 5.3. The supercomponent evidence value is 0.38 because "tcanoutf" belongs to the trash can ASSEMBLY. The maximum of the other SURFACE plausibility values for non-generically related identities is 0.41 (for the "robbodyside" model), so this causes inhibition. These evidence values are now integrated to give the final plausibility value for "tcanoutf" as 0.62. As this is positive, the trash can outer surface model will be invoked for this region.

We now consider the problem of invoking the trash can ASSEMBLY model in surface cluster 8 (from Table 5.1), which is composed of exactly the trash can's outer and inner surface regions. For each of the two surfaces, three possible identities obtain: trash can inner surface, trash can outer surface and trash can bottom. The trash can model specifies only subcomponent and inhibition relationships and defines three subcomponents:

$$\vbox{\hskip 0.5in \begin{tabular}{cc} SUBCOMPONENT&WEIGHT ... ...ne tcanoutf&0.9\\ tcaninf&0.6\\ tcanbot&0.4\\ \end{tabular}}$$

These are organized into three visibility groups:

    SUBCGRP OF trashcan = tcanoutf tcaninf;
    SUBCGRP OF trashcan = tcanoutf tcanbot;
    SUBCGRP OF trashcan = tcaninf tcanbot tcanoutf;

The plausibilities of the subcomponent model SURFACE instances are:

	DATA INNER	DATA OUTER
MODEL INNER	-0.42	0.26
MODEL OUTER	-0.48	0.62
MODEL BOTTOM	-0.81	-0.88

The subcomponent evidence computation starts with the best plausibility for each model feature: inner = 0.26, outer = 0.62, bottom = -0.81. (Note that, because of occlusion, the data outer surface provides better evidence for the model inner SURFACE that the data inner surface, because all properties other than maximum curvature are shared. This does not cause a problem; it only improves the plausibility of the inner SURFACE model.) The visibility group calculation used the harmonic mean with the weightings given above to produce a subcomponent evidence value of 0.46, -0.08 and 0.01 for the three visibility groups. Finally, the best of these was selected to give the subcomponent evidence of 0.46.

The highest competing identity was from the robbody model, with a plausibility of 0.33. Integrating these evidence values gives the final plausibility for the trash can as 0.38, which was the supercomponent plausibility used in the first example.

Because there are far too many plausibility and evidence values to describe the whole network, even for this modest model base (16 ASSEMBLYs, 25 SURFACEs, and 24 generic descriptions: 22 for SURFACEs and 2 for ASSEMBLYs), we next present a photograph of the network to illustrate the general character of the computation, and then look at the invoked model instances in more detail. Figure 8.14 shows all model instance nodes of the network in its converged state. In the large region at the upper left of the picture (with the textured appearance) each small grey colored rectangle represents one model instance. The brightness of the box encodes its plausibility, from black ($-1.0$) to white ($+1.0$). The model instances are represented in a two dimensional grid, indexed by the image features horizontally from left-to-right with surfaces first and then the surface clusters. The vertical index lists the model features from top to bottom, with model SURFACEs and then ASSEMBLYs. The two large black areas on the upper right and lower left arise from type incompatibility (model SURFACEs with surface clusters on the upper right and ASSEMBLYs with image surfaces on the lower left). The cover jacket of the book shows the results of the network more clearly, by encoding the plausibility from blue ($-1.0$) to red ($+1.0$).

Figure 8.14: Model Instance Node Summary after Convergence

Several interesting features can be seen immediately. First, there is a strong horizontal grouping of black and white boxes near the middle of the upper left surface pairing nodes. These are for the generic description evidence types, such as planar, positive cylinder, etc. As they are defined by only a few properties, they achieve strong positive or negative plausibilities. The specific model SURFACEs are above, and other generic SURFACE features are below these. Only the specific model SURFACEs can be invoked, and there are only a few bright-grey to white nodes with a plausibility that is high enough for this, whereas there are many darker grey low plausibility nodes (more details below).

A similar pattern is seen in the ASSEMBLY nodes on the lower right, except for a large brightish region on the right side, with many potentially invokable model instances. This bright region occurs because: (1) there are several nested surface clusters that all contain much of the robot and (2) a surface cluster containing most of an object generally acquires a high plausibility for the whole object. This led to the explicit disabling of model instance nodes after verification, as described previously.

All invocations for this image are summarized in Tables 8.1 and 8.2 (surface clusters are listed in Table 5.1 and image regions are shown in Figure 3.10). As commented above, successful invocations in one context mask invocations in larger containing contexts. Further, generic models are not invoked - only the object-specific models. Hence, not all positive final plausibilities from Figure 8.14 cause invocation.

ASSEMBLY invocation is selective with 18 invocations of a possible 288 (16 ASSEMBLY models in 18 surface cluster contexts). Of these, all appropriate invocations occur, and nine are in the smallest correct context and one is in a larger context. Of the others, three are justified by close similarity with the actual model (note 1 in the table) and five are unjustified (notes 2 and 3).

SURFACE model invocation results are similar, with 21 invocations out of 475 possible (25 SURFACE models in 19 surface contexts). Of these, ten were correct, five are justifiably incorrect because of similarity (note 1) and six are inappropriate invocations (notes 2 and 3).

Table 8.1: Invoked ASSEMBLY Model Hypotheses

MODEL	SURFACE CLUSTER	PLAUSIBILITY	INVOCATION STATUS	NOTES
robshldbd	3	0.50	E
robshldsobj	5	0.45	E
robshldsobj	2	0.44	I	2
robshldsobj	11	0.44	I	2
robshould	11	0.39	E
trashcan	8	0.38	E
robbody	12	0.33	I	1
robbody	13	0.33	I	1
robbody	8	0.33	I	1
robbody	15	0.33	L
lowerarm	7	0.29	E
link	15	0.15	E
robot	14	0.14	I	3
robot	15	0.14	E
link	17	0.11	I	3
armasm	13	0.09	E
upperarm	9	0.05	E
robot	17	0.02	I	3

STATUS
E	invocation in exact context
L	invocation in larger than necessary context
I	invalid invocation
NOTES
1	because true model is very similar
2	ASSEMBLY with single SURFACE has poor discrimination
3	not large enough context to contain all components

Table 8.2: Invoked SURFACE Model Hypotheses

MODEL	SURFACE REGION	PLAUSIBILITY	INVOCATION STATUS	NOTES
robshldend	26	0.76	C
tcanoutf	9	0.61	C
robbodyside	9	0.41	I	1
robshoulds	29	0.40	C
robshoulds	27	0.40	I	3
ledgea	18	0.36	C
lendb	31	0.27	C
tcaninf	9	0.26	I	1
ledgeb	18	0.25	I	1
robshould1	16	0.21	I	1
robshould2	16	0.21	C
lsidea	12	0.20	I	1
lsideb	12	0.20	C
robbodyside	8	0.11	C
robshould1	12	0.10	I	3
robshould2	12	0.10	I	3
uside	19,22	0.07	C
uedgeb	19,22	0.07	I	2
lsidea	19,22	0.04	I	2
lsideb	19,22	0.04	I	2
uends	25	0.02	C

STATUS
C	correct invocation
I	invalid invocation
NOTES
1	because of similarity to the correct model
2	because the obscured correct model did not inhibit
3	because of some shared characteristics with the model

Clearly, for this image, the invocation process works well. The chief causes for improper invocation were:

1. combinatorial surface cluster formation, resulting in similar but not directly related contexts which are thus not inhibited by the correct context, and
2. superficial similarity between features.

Possible solutions to these problems are:

• improving the depth merged surface cluster formation process and
• increasing the number of object properties.