

Next: Euclidean Distance in Wavelet
Up: Introduction to Wavelet Networks
Previous: Direct Calculation of Weights
Considering the optimized family of wavelets 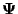 , its closed
linear span constitutes a subspace
, its closed
linear span constitutes a subspace
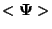 in the
in the
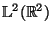 space.
With eq. (8) any
function can be orthogonally projected into that subspace. It is
interesting to ask whether
space.
With eq. (8) any
function can be orthogonally projected into that subspace. It is
interesting to ask whether 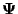 constitutes a basis, because then
the projection is unique. That this is indeed
so can be shown with induction over the number of wavelets:
Consider
constitutes a basis, because then
the projection is unique. That this is indeed
so can be shown with induction over the number of wavelets:
Consider 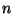 wavelets
wavelets
 , that minimize
the energy functional (2) and that form a
basis. Let us choose a new wavelet that approximates best the
residual between the function
, that minimize
the energy functional (2) and that form a
basis. Let us choose a new wavelet that approximates best the
residual between the function 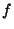 and its approximation with the first
and its approximation with the first 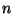 wavelets. After optimization of the
wavelets. After optimization of the
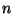 th
th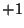 wavelet,
the energy functional (2) is smaller than
before (for the
wavelet,
the energy functional (2) is smaller than
before (for the 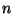 wavelets):
Assuming now, that
we have in particular
This again means that
which implies
This, however, contradicts the choice of
wavelets):
Assuming now, that
we have in particular
This again means that
which implies
This, however, contradicts the choice of
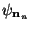 in the
optimization step, where
in the
optimization step, where
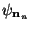 was selected such that
was selected such that
Let us call the closed linear span of
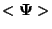
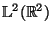 (image)
subspace. The dual wavelets
(image)
subspace. The dual wavelets
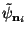 are linearly
independent, and the projection
are linearly
independent, and the projection
establishes an isomorphism from
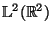 (or the image space, respectively) into
(or the image space, respectively) into
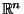 which is the space of the
which is the space of the 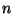 -vectors containing the
wavelet coefficients. This space is dual to the image
subspace and we call it the wavelet subspace.
-vectors containing the
wavelet coefficients. This space is dual to the image
subspace and we call it the wavelet subspace.


Next: Euclidean Distance in Wavelet
Up: Introduction to Wavelet Networks
Previous: Direct Calculation of Weights
Volker Krueger
2001-05-31
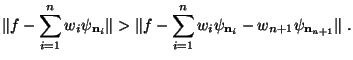
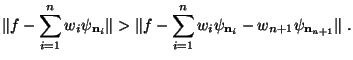
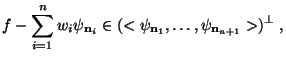
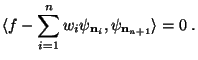
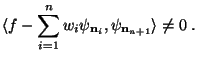
![]()
![]() (image)
subspace. The dual wavelets
(image)
subspace. The dual wavelets
![]() are linearly
independent, and the projection
are linearly
independent, and the projection