

Next: Wavelet basis and Wavelet
Up: Introduction to Wavelet Networks
Previous: Introduction to Wavelet Networks
Direct Calculation of Weights
Wavelet functions are not necessarily orthogonal. For a given family
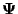 of wavelets it is therefore not generally possible
to calculate a wavelet coefficient
of wavelets it is therefore not generally possible
to calculate a wavelet coefficient 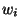 directly by a simple projection of the
wavelet
directly by a simple projection of the
wavelet
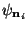 onto the considered function. In
[Daubechies, 1990,Daugman, 1988] it was therefore proposed to use
eq. (2) to find the optimal coefficients
onto the considered function. In
[Daubechies, 1990,Daugman, 1988] it was therefore proposed to use
eq. (2) to find the optimal coefficients 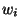 for each
fixed wavelet. Because optimization is a slow process, we want to suggest a
direct calculation for the case of a finite wavelet family.
The correct coeffs.
for each
fixed wavelet. Because optimization is a slow process, we want to suggest a
direct calculation for the case of a finite wavelet family.
The correct coeffs.
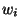 are computed by projecting the dual wavelets
are computed by projecting the dual wavelets
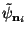 .
The wavelet
.
The wavelet
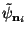 is the dual wavelet to the
wavelet
is the dual wavelet to the
wavelet
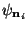 if
if
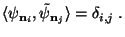 |
(4) |
With
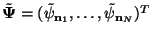 ,
we can write
,
we can write
![$\displaystyle \left[\left<{\bf\Psi},\tilde{{\bf\Psi}}\right>\right]={\rm 1\negthickspace I}$](img58.gif) |
(5) |
and we find
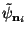 to be
to be
 |
(6) |
where
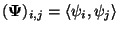 .
Given a family
.
Given a family 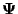 of optimized wavelets of a WN for the function
of optimized wavelets of a WN for the function
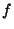 , we can compute the orthogonal projection of a function
, we can compute the orthogonal projection of a function  into the subspace
into the subspace
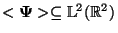 (see
(4)), i.e.
(see
(4)), i.e.
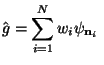 with with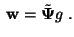 |
(7) |
The method to compute the orthogonal projection of a function  into
the subspace
into
the subspace
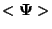 is mathematically equivalent to using the
pseudo-inverse of
is mathematically equivalent to using the
pseudo-inverse of 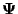 directly. However, using the dual wavelets
of eq. (7) will proof to be computationally more
efficient: For our tracking experiment we will have to deform the
entire WN affinely,
which means that the pseudo-inverse has to be recomputed. The matrix
directly. However, using the dual wavelets
of eq. (7) will proof to be computationally more
efficient: For our tracking experiment we will have to deform the
entire WN affinely,
which means that the pseudo-inverse has to be recomputed. The matrix
 , on the other hand, is invariant, except for a factor,
to affine deformations of the WN, and only the projections
, on the other hand, is invariant, except for a factor,
to affine deformations of the WN, and only the projections
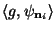 need to be recomputed.
need to be recomputed.


Next: Wavelet basis and Wavelet
Up: Introduction to Wavelet Networks
Previous: Introduction to Wavelet Networks
Volker Krueger
2001-05-31
![]() into
the subspace
into
the subspace
![]() is mathematically equivalent to using the
pseudo-inverse of
is mathematically equivalent to using the
pseudo-inverse of ![]() directly. However, using the dual wavelets
of eq. (7) will proof to be computationally more
efficient: For our tracking experiment we will have to deform the
entire WN affinely,
which means that the pseudo-inverse has to be recomputed. The matrix
directly. However, using the dual wavelets
of eq. (7) will proof to be computationally more
efficient: For our tracking experiment we will have to deform the
entire WN affinely,
which means that the pseudo-inverse has to be recomputed. The matrix
![]() , on the other hand, is invariant, except for a factor,
to affine deformations of the WN, and only the projections
, on the other hand, is invariant, except for a factor,
to affine deformations of the WN, and only the projections
![]() need to be recomputed.
need to be recomputed.