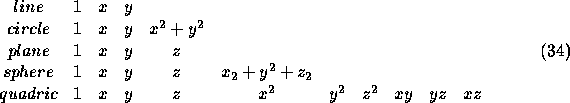
Shapes or surfaces can be defined by a basis set of generators, for example

It can be shown that in general it is possible to compute an exact fit of a shape of basis set of size n to n-1 points. For example, we can fit a line to two points, a circle to three points, a plane to three points and so on. To express this, we can use the general form of the least squares problem (``Solving least squares problems'' by Lawson and Hanson, 1974). i.e. 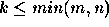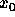given a real m by n matrix A of rank and given a real m-vector b, find a real n-vector which minimises the Euclidean length of Ax-b. ( a matrix has rank, k, if it contains at least one k-rowed submatrix with non vanishing determinant, while the determinant of any square matrix having k+1 or more rows, possibly contained in A is zero. )

For an exact fit, Rank(A) = m = n and the equation becomes

A is the matrix defining the coordinates of the measured data. x is the parameter vector and b is the measured data vector. For example, in a depth image, A contains the sets of 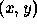coordinates and a constant term, normalised to 1 for convenience, and b is the measured depth data or z values. For a plane,

This allows three linear equations of the form of Equation 2 with three unknowns, i.e. a,b and c and can thus be solved by conventional techniques. Pratt (``Direct least square fitting of algebraic surfaces'', Computer Graphics 21,(4) pp145-151 (1987)) suggests the following general approach. However, note that we can also compute an equivalent solution

Define a square matrix 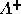from A by adding a final row consisting of the basis polynomials themselves, and form the determinant.

In this case, the equation of the fitted plane is