Binary Images

Binary images are images that have been quantised to two values, usually denoted 0 and 1, but often with pixel values 0 and 255, representing black and white.

Binary images are used in many applications since they are the simplest to process, but they are such an impoverished representation of the image information that their use is not always possible. However, they are useful where all the information you need can be provided by the silhouette of the object and when you can obtain the silhouette of that object easily.

Some sample application domains include

• identifying objects on a conveyor -- for example, sorting chocolates!
• identifying orientations of objects, and
• interpreting text.

Sometimes the output of other image processing techniques is represented in the form of a binary image, for example, the output of edge detection can be a binary image (edge points and non-edge points). Binary image processing techniques can be useful for subsequent processing of these output images.

Binary images are typically obtained by thresholding a grey level image. Pixels with a grey level above the threshold are set to 1 (equivalently 255), whilst the rest are set to 0. This produces a white object on a black background (or vice versa, depending on the relative grey values of the object and the background). Of course, the `negative' of a binary image is also a binary image, simply one in which the pixel values have been reversed.

However, choosing a threshold can be difficult, and is even considered by some [1] to be a `black art'. Most approaches make use of the histogram of the number of times each grey level occurs in the image. If you are fortunate the histogram will be bimodal and choosing a threshold manually will be easy. It may even be possible to construct an automatic procedure to determine it. Ideally, if we had a black object on a white background the histogram should appear as in figure 1.

 

Figure 1: The ideal histogram of a light object on a darker plain background.

But we have measurement noise. The histogram we end up seeing is the result of convolving the `ideal' histogram with the probability distribution of the noise.

 

Figure 2: The histogram of an image showing the frequency of occurrence of each grey scale value.

If the grey levels of the object and the background are fairly close the influence of noise may result in the object only appearing as a `shoulder' in the histogram.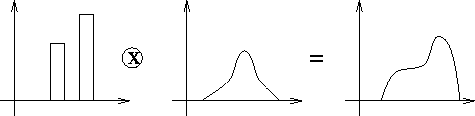

 

Figure 3: When background and object are close in grey levels, thresholding is difficult to determine automatically.

In this case the histogram will no longer be bimodal. There will be no clear way of choosing the threshold. Repeated observations and averaging may help, but the spread of the histogram may be due to lighting variations or colour variations in the background and object.

Analysis of Binary Images

We wish to determine various attributes of the objects in the scene with the aim of using these to identify the objects and to determine their position and orientation. We define the characteristic function of an object in an image to be

$$b(x,y) \left\{ \begin{array} {ll} = 1 & \mbox{for points on... ...ct} \\ = 0 & \mbox{for background points.}\end{array} \right.$$

 

Figure 4: A binary image.

Now consider the image to be continuous (that is, to have infinite resolution).

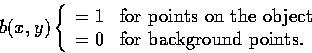
The area is given by the 0^th moment of the object:

$$A = \int \int b(x,y) dx dy.$$

The centre of mass, denoted by $(\overline{x},\overline{y}),$ is given by the 1^st moments of the object:

$$\overline{x} = \frac{\int \int x b(x,y)dxdy}{ \int \int b(x,y)dxdy},$$

and

$$\overline{y} = \frac{\int \int y b(x,y)dxdy}{ \int \int b(x,y)dxdy}.$$

Generally we use the axis of minimum inertia of the object to identify the orientation. This is the axis of least 2^nd moment.

 

Figure 5: The 0^th moment is the area of the object; the 1^st moment gives the centre of mass; and the 2^nd moments give the axes of orientation.

We want to find the line for which the integral

$$I = \int \int r^{2} b(x,y) dx dy$$

is a minimum, where r is the perpendicular distance from (x,y) to the line we want to find (see figure 6).

The solution for the equation of this line is made more convenient if we parametrise the line using

$$x \sin\theta - y \cos\theta + \rho = 0.$$

 

Figure 6: Parametrising a line by its angle with the x-axis and its distance from the origin.

Thus we have to solve for the $\theta$ and $\rho$ that will give the axis of least second moment. Why do we specify the line like this?

Given this equation we can write parametric equations for points on the line as follows:

$$x_{0} = - \rho \sin\theta + t \cos\theta,$$

and

$$y_{0} = \rho \cos\theta + t \sin\theta,$$

where t is the distance along the line from the closest point to the origin.

Given a point (x,y) we need to find the closest point on the line so that we can calculate the distance r, which is given by (see figure 6)

r² = (x - x₀)² + (y - y₀)².

We substitute for x₀ and y₀ to get

$$r^{2} = x^{2} + y^{2} + \rho^{2} + 2\rho (x \sin\theta - y\cos\theta) - 2 t(x\cos\theta + y\sin\theta) + t^{2}.$$

What value of t minimizes this expression?

Differentiating with respect to t and equating the result to 0 gives

$$t = x\cos\theta + y\sin\theta.$$

So we substitute this back into a parametric equations for x₀ and y₀. This gives

and likewise for y - y₀.

Thus r² can be written as

$$r^{2} = (x\sin\theta - y\cos\theta + \rho)^{2}.$$

This line is the locus of points for which r = 0. Hence, by parametrising the line in this manner we can obtain the distance from the line directly.

Solving for $\rho$ and $\theta$

We now want to find the $\rho$ and $\theta$ that describe the line that minimizes distances of points in the object to that line, that is, that minimizes

$$I = \int \int (x\sin\theta - y\cos\theta + \rho)^{2} b(x,y)dx dy.$$

We differentiate with respect to $\rho$ and set the resulting expression to 0, giving

$$\int \int 2(x\sin\theta - y\cos\theta + \rho) b(x,y)dx dy = 0,$$

which is just

$$\int \int x\sin\theta b(x,y)dx dy - \int \int y\cos\theta b(x,y)dx dy + \int \int \rho b(x,y)dx dy = 0.$$

Multiplying and dividing by $A = \int \int b(x,y)dx dy$ gives

$$A \left( \frac{\int \int x\sin\theta b(x,y)dx dy}{\int \int ... ...nt \int \rho b(x,y)dx dy} {\int \int b(x,y)dx dy} \right) = 0,$$

and this is just

$$A(\overline{x} \sin\theta - \overline{y} \cos\theta + \rho) = 0,$$

where $\overline{x}$, $\overline{y}$ is the centre of mass. That is, the axis of minimum 2nd moment passes through the centre of mass.

We now have to find the value of $\theta$ that minimizes I. To do this, we change coordinates so that we are now working with respect to the centre of mass:

This simplifies the equation of our line to

$$x\sin\theta - y\cos\theta + \rho = x'\sin\theta - y'\cos\theta,$$

and so

$$I = \int \int (x'\sin\theta - y'\cos\theta)^{2}b(x',y')dx' dy'$$

$$\Rightarrow I = a \sin^{2}\theta - b \sin\theta\cos\theta + c \cos^{2}\theta,$$

where

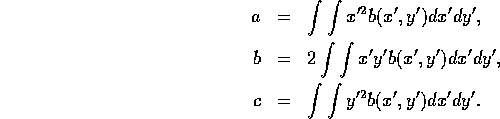
The constants a, b, and c are called the second moments.

If we use the substitutions $b\sin\theta\cos\theta = \frac{b}{2}\sin 2\theta$ and $\cos 2\theta = 2\cos^{2}\theta -1$, then

Thus

$$I = \frac{1}{2}(c+a) - \frac{1}{2}(a-c)\cos 2\theta - \frac{1}{2}b\sin 2\theta.$$

We differentiate this expression with respect to $\theta$ and set the result to 0, obtaining

$$(a-c) \sin 2\theta - b \cos 2\theta = 0,$$

which implies

$$\tan 2\theta = \frac{b}{a-c},$$

unless b = 0 and a=c.

Thus

$$\frac{\sin^{2}2\theta}{\cos^{2}2\theta} = \frac{b^{2}}{(a-c)^{2}},$$

which implies that

$$\frac{\sin^{2}2\theta}{ 1 - \sin^{2}2\theta} = \frac{b^{2}}{(a-c)^{2}}.$$

This is just a quadratic in $\sin^2(2\theta)$, so we see that it has solution

$$\sin 2\theta = \frac{ \pm b}{\sqrt{b^{2} + (a-c)^{2}}},$$

and

$$\cos 2\theta = \frac{ \pm (a-c)}{\sqrt{b^{2} + (a-c)^{2}}}.$$

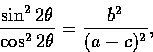
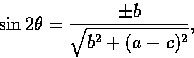
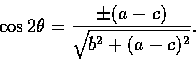
When one chooses the positive solution, this minimizes I; when one chooses the negative solution, this maximizes I.

In the case that b=0 and a=c we see that I is unaffected by the direction of axis of orientation, that is, our object is rotationally symmetric.

The ratio $\frac{I_{min}}{I_{max}}$ gives us some idea of how rounded the object is. This ratio will be 0 for a line and 1 for a circle.