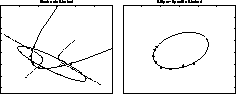
Figure: Specificity to ellipses. The three eigen-solution obtained by the Bookstein algorithm (left) and the best LSQ elliptical solution obtained by our ellipse-specific method (right).
Figure: Specificity to ellipses. The three eigen-solution
obtained by the Bookstein algorithm (left) and
the best LSQ elliptical solution obtained
by our ellipse-specific method (right).
First, let us now have a glimpse at what this ellipse-specificity
means. Figure 
-left shows the three
eigen-solutions yielded by the Bookstein algorithm on a small set of
hand-input points; the best LSQ fit is a hyperbola and the
(incidentally) elliptical one is extremely poor. With the proposed
ellipse-specific algorithm, the only solution satisfying the constraint
is the best LSQ elliptical solution, shown in Figure
-right.
Figure shows three experiments designed after
[10] that consist of the same parabolic data but with
different realizations of added isotropic Gaussian noise (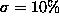
of data spread). In his paper, Sampson refined the poor initial
fitting obtained with Bookstein algorithm using an iterative Kalman
filter to minimise his approximate geometrical distance
[10]. The final results were ellipses with low eccentricity
that are qualitatively similar to those produced by our
ellipse-specific direct method (solid lines) but at the same
computational cost of producing Sampson's initial estimate.
The low-eccentricity bias of our method discussed in
Section. 3 is most evident in Figure
when comparing the results to other methods, namely Bookstein
(dotted), Taubin (dash-dots) and Gander (dashed); these results are
not surprising, since those methods are non-ellipse specific whereas
the one presented here is.
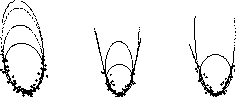
Figure: Low-eccentricity bias of the ellipse-specific method
when fitting to noisy parabolic data. Encoding is
Bookstein: dotted; Gander: dashed; Taubin: dash-dot;
Ellipse-specific: solid.
Let us now qualitatively illustrate the robustness of the
ellipse-specific method as compared to Gander's and Taubin's. A
number of experiments have been carried out, of which here we present
a couple, shown in Figures and . They
have been conducted by adding isotropic Gaussian noise to a synthetic
elliptical arc; note that in both sets each column has the same
set of points. More quantitative results can be found in
[2] and are not reported here for reasons of space.
Figure shows the performance with respect to
increasing noise level (see [3] for more experiments).
The standard deviation of the noise varies from 3% in the leftmost
column to 20% of data spread in the rightmost column; the noise has
been set to relatively high level because the performance of the three
algorithm is substantially the same at low noise level of
precise elliptical data. The top row shows the results for the
method proposed here. Although, as expected, the fitted ellipses
shrink with increasing levels of high noise (as a limit the elliptical
arc will look like a noisy line), it can be noticed that the ellipse
dimension decreases smoothly with the increase of noise level: this is
an indication of well-behaved fitting. This shrinking phenomenon is
evident also with the other two methods but presents itself more
erratically: in the case of Taubin's algorithm, the fitted ellipses are
on average somewhat closer to the original one [3],
but they are rather unpredictable and its ellipse non-specificity, as
it happens in the Gander's case, sometimes yields unbounded hyperbolic
fits.
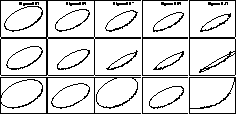
Figure: Stability experiments with increasing noise level.
Top row: ellipse-specific method; Mid Row: Gander;
Bottom Row: Taubin. The ellipse-specific method
shows a much smoother and predictable decrease in
quality than the other two methods.
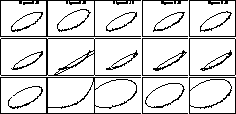
Figure: Stability experiments for different runs with same
noise variance (10% of data spread).
Top row: ellipse-specific method; Mid Row: Gander;
Bottom Row: Taubin. The ellipse-specific method
shows a remarkable stability.
The second set, shown in Figure , is concerned with
assessing stability to different realizations of noise with the
same variance (
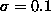). (It is very desirable that an
algorithm's performance be affected only by the noise level, and not
by a particular realization of the noise). This and similar
experiments (see [2,3]) showed that our method has a
remarkably greater stability to noise with respect to Gander's and
Taubin's.