Let us consider the following one-dimensional signal ![]() . It assumes values
. It assumes values ![]() , the plot of which is shown in Figure 1 a. The corresponding Fourier transform is function P(f) visualized in Figure 1 b. The total duration of the signal is T=17.
, the plot of which is shown in Figure 1 a. The corresponding Fourier transform is function P(f) visualized in Figure 1 b. The total duration of the signal is T=17.
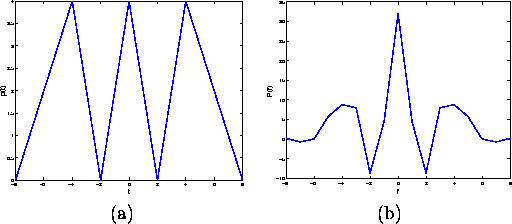
Figure 1: Original signal p(t) (a) and its Fourier transform P(f) (b).
Let us consider a regular subsampling of the original signal p(t), ![]() . It assumes values
. It assumes values ![]() . The regular sampling pattern used is
. The regular sampling pattern used is ![]() , the values of which are
, the values of which are ![]() .
.
The sampled values are shown as magenta circles in Figure 2 a. The total number of regular samples is N=9. The DFT of the regularly sampled signal is plotted in Figure 2 b in magenta superimposed to the Fourier transform of the original signal in blue. It is possible to notice that the Fourier transform of the regularly sampled signal has the same shape of the original Fourier transform, the peaks are slightly lower (the signal loses some energy) and the higher frequencies are missing, in fact only half of the Fourier coefficients are present.
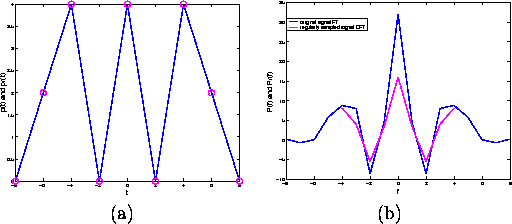
Figure 2: Regularly sampled signal ![]() superimposed on the original signal p(t) (a) and its Discrete Fourier transform (DFT)
superimposed on the original signal p(t) (a) and its Discrete Fourier transform (DFT) ![]() (in magenta) superimposed on the Fourier transform of the original signal (in blue)(b).
(in magenta) superimposed on the Fourier transform of the original signal (in blue)(b).
If we Fourier transform the ![]() back, which is to say we use the inverse DFT, we obtain the original signal p(t) if the regular sampling frequency is above the Nyquist limit of twice the highest frequency present in the original signal. A smoothed (low-pass) approximation of the original signal is obtained, if the Nyquist condition is not met. In the case of N=9 the Nyquist condition is respected and the signal is reconstructed perfectly as shown in Figure 3. In the case the number of samples is lowered and therefore the sampling interval increases, the reconstruction is imperfect as shown from the examples in Figure 4 a for N=8 and Figure 4 b for N=6.
back, which is to say we use the inverse DFT, we obtain the original signal p(t) if the regular sampling frequency is above the Nyquist limit of twice the highest frequency present in the original signal. A smoothed (low-pass) approximation of the original signal is obtained, if the Nyquist condition is not met. In the case of N=9 the Nyquist condition is respected and the signal is reconstructed perfectly as shown in Figure 3. In the case the number of samples is lowered and therefore the sampling interval increases, the reconstruction is imperfect as shown from the examples in Figure 4 a for N=8 and Figure 4 b for N=6.
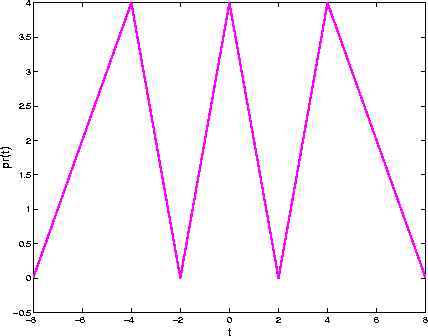
Figure 3: Reconstructed signal using the inverse Fourier Transform (IDFT) using N=9 regularly spaced samples.
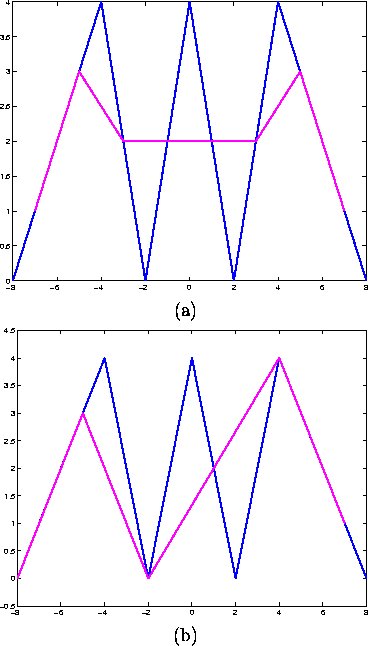
Figure 4: Reconstruction of the original signal (in blue) using N=8 regularly spaced samples (a) and N=6 regularly spaced samples (b). The reconstruction is not perfect because the number of samples is reduced.