Now we want to reconstruct the signal p(t) from a collection of samples taken irregularly using the inverse Fourier transform. Let us take into consideration an irregular sampling 
of the original signal p(t). The number of samples taken into consideration is the same as in the case of the regular sampling, N=9.
The irregular sampling sequence is 
, so these are the irregular sampling coordinates that have to be used in the computation of the NDFT. The irregular samples are shown as green circles in Figure 5 a and the corresponding NFT is shown as the green curve in Figure 5 b.
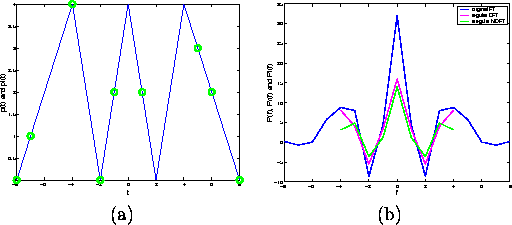
Figure 5: Irregularly sampled signal 
superimposed on the original signal p(t) (a) and its Nonuniform Discrete Fourier transform (NDFT) 
(in green) superimposed to the Fourier transform of the original signal, P(f) (in blue) and the DFT of the regularly sampled signal, 
(in magenta) (b).
Now it is possible to calculate the regular inverse DFT of the Fourier transform , which provides a reconstruction 
of the original signal p(t). This reconstruction is shown in green in Figure 6, superimposed to the original signal in blue.
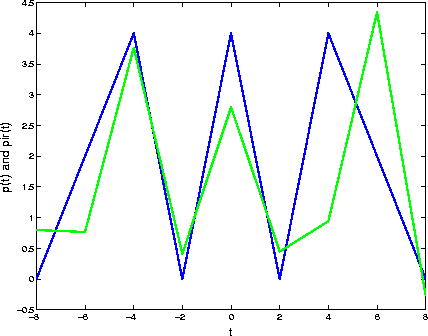
Figure 6: Reconstructed signal using the inverse Fourier Transform (IDFT) of the NDFT .
The reconstructed signal has the same shape of the original signal and provides a good approximation, however it is not an interpolation of the original signal, as the values of the original signal at the sampling points are not recovered.
Let us make a comparison now between the computation of the DFT and the computation of the NDFT. For the computation of the DFT it is necessary to calculate the matrix:
where 
is the transpose of vector 
which contains the N=9 indices of the Fourier coefficients. The coefficients obtained by the multiplication 
are shown in Figure 7 a.
Using a matrix formulation the calculation of the DFT 
can be expressed as:
In order to compute the NDFT it is necessary to calculate the matrix:
where 
is the transpose of vector 
which contains the N=9 coordinates of the irregular sampling sequence. Once again, we remind that T=17 is the total length of the signal p(t). The coefficients obtained by the multiplication 
are shown in Figure 7 b.
Using a matrix formulation the calculation of the NDFT 
can be expressed as:
Inspection of Figure 7 helps visualize the difference in the two matrices used for the regular and irregular calculation of the Fourier transform. Each line in the diagrams on Figure 7 corresponds to a matrix row. The regular circles in Figure 7 a correspond to the column values as column index assumes the N=9 values from -4 to 4. In Figure 7 b the N=9 cross values are placed irregularly and their position is dependent on the sampling sequence represented by vector .
By using these coefficients as exponents of the exponential Fourier kernel, the complex values shown in Figure 8 are obtained. The values of the Fourier exponential functions in the regular matrix are shown as magenta circles on the complex plane, while the corresponding functions for the irregular matrix are shown as green crosses in the complex plane. Since matrices 
and 
are square matrices of dimension N, one would expect to see 
values. Since the values shown are much fewer, this means that some values are assumed by elements of the matrices more than once.
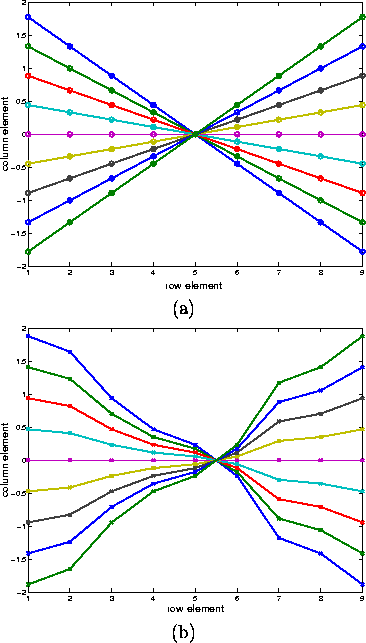
Figure 7: Regular matrix coefficients obtained from the vector multiplication (a) and irregular matrix coefficients obtained from the vector multiplication (b) as row and colum values of a matrix.
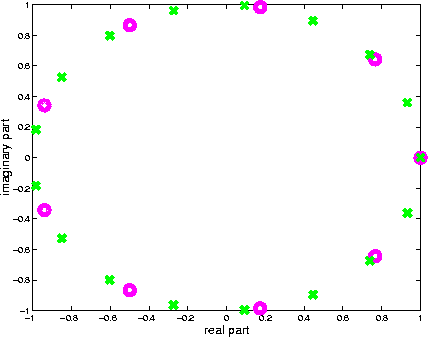
Figure 8: Values assumed by the elements of the regular matrix in magenta and of the irregular matrix in green, in the complex plane.