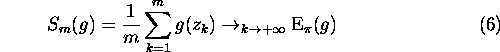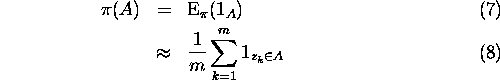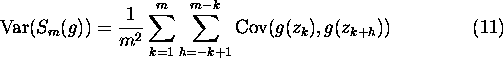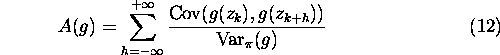

Next: Sampling algorithms
Up: An introduction to Markov
Previous: Markov chains on countable
²
The extensive use of Markov chains in statistical applications relies on the possibility of estimating the properties of a probability distribution  through Monte Carlo sampling. Indeed, let us assume that we want to compute the expectation under
through Monte Carlo sampling. Indeed, let us assume that we want to compute the expectation under  of a function g defined on F:
of a function g defined on F:
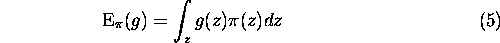
where g is a  -measurable function. The law of the large number ensures that the arithmetic mean of an independent sample
-measurable function. The law of the large number ensures that the arithmetic mean of an independent sample 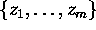 with distribution
with distribution  converges towards the integral:
converges towards the integral:
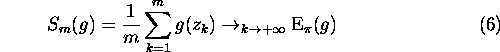
This is the principle of Monte Carlo integration: each time we want to estimate a (possibly highly dimensional) integral under the distribution  , we sample the distribution
, we sample the distribution  and compute the arithmetic mean. Especially, the probability under
and compute the arithmetic mean. Especially, the probability under  of any particular event can be computed:
of any particular event can be computed:
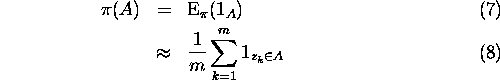
A nice feature about Monte Carlo integration is that the approximation in equation 6 does not depend on the dimension of the state space, but only on the size of the sample. Indeed, under the assumption of independence, the variance of the estimate 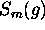 of equation 6 writes:
of equation 6 writes:
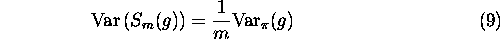
What happens if we now sample the distribution  with a Markov chain Z? The main difference is that the samples are no longer independent since consecutive states of a Markov chain are linked by the transition kernel K. However, if Z is an irreducible ergodic Markov chain with stationary distribution
with a Markov chain Z? The main difference is that the samples are no longer independent since consecutive states of a Markov chain are linked by the transition kernel K. However, if Z is an irreducible ergodic Markov chain with stationary distribution  , the ergodic theorem implies the convergences of the sample means [5]:
, the ergodic theorem implies the convergences of the sample means [5]:

The variance of the estimate 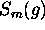 now depends on the correlation between consecutive states of the chain:
now depends on the correlation between consecutive states of the chain:
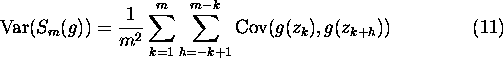
Let us define the integral range as the sum of the correlations [7, 8]:
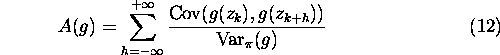
The variance of the estimate 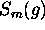 can then be approximated by:
can then be approximated by:
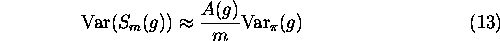
Hence, the larger the integral range, the larger the size m of the sample needs to be to obtain an estimate of the same quality of the independent estimate. The choice of the transition kernel K controls the convergence properties of the Monte Carlo integrals and is very important in practice. Transition kernels which increase the mixing within the chain (and thus decrease the correlation between consecutive states) must be preferred.


Next: Sampling algorithms
Up: An introduction to Markov
Previous: Markov chains on countable
Bob Fisher
Fri Jul 26 09:56:32 BST 2002