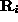 ;
Suppose that we have obtained projective camera motion
;
Suppose that we have obtained projective camera motion 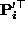 by factoring the measurement matrix. Since the intrinsic camera
parameters are assumed to be known, we can set
by factoring the measurement matrix. Since the intrinsic camera
parameters are assumed to be known, we can set
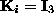 . Then, substituting
(1) into (13)
and eliminating
. Then, substituting
(1) into (13)
and eliminating 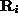 , we have
, we have



The metric constraints for perspective cameras are also derived based on
the orthogonality of the camera orientation matrix 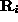 ;
Suppose that we have obtained projective camera motion
;
Suppose that we have obtained projective camera motion 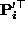 by factoring the measurement matrix. Since the intrinsic camera
parameters are assumed to be known, we can set
by factoring the measurement matrix. Since the intrinsic camera
parameters are assumed to be known, we can set
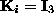 . Then, substituting
(1) into (13)
and eliminating
. Then, substituting
(1) into (13)
and eliminating 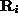 , we have
, we have
where 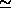 stands for equality up to an unknown non-zero scale. Let
stands for equality up to an unknown non-zero scale. Let
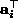 ,
, 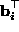 and
and  are three rows of
are three rows of
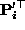 , and
, and  be a 4
be a 4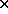 3 matrix composed
from the first three columns of
3 matrix composed
from the first three columns of  . Then
(25) can be rewritten as
. Then
(25) can be rewritten as
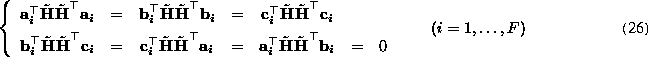
which gives 5F linear homogeneous equations in terms of 10 elements of
the 4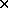 4 symmetric matrix
4 symmetric matrix 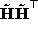 and can be
solved for
and can be
solved for 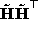 in the least-squares sense.
Since
in the least-squares sense.
Since  is a 4
is a 4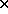 3 matrix,
3 matrix,
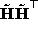 cannot be full rank and one of its
eigenvalues is zero. Therefore its eigenvalue decomposition has the
form:
cannot be full rank and one of its
eigenvalues is zero. Therefore its eigenvalue decomposition has the
form: 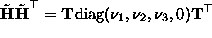 where
where 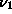 ,
, 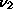 and
and 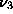 are
non-negative eigenvalues of
are
non-negative eigenvalues of  , and
, and
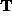 is a 4
is a 4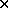 4 orthogonal matrix. Letting
4 orthogonal matrix. Letting 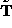 be a 4
be a 4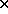 3 matrix taking first three columns of
3 matrix taking first three columns of 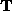 , we
then obtain
, we
then obtain  as
as 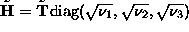 .
.
Since the fourth column of  affects only the translation
and isometric scaling, it can be set to an arbitrary non-zero 4-vector.
Thus, we have determined a projective transformation
affects only the translation
and isometric scaling, it can be set to an arbitrary non-zero 4-vector.
Thus, we have determined a projective transformation  with
which projective motion and shape are upgraded to Euclidean
descriptions.
with
which projective motion and shape are upgraded to Euclidean
descriptions.