Substituting
(3) into
(9) and eliminating  using
its orthogonality, we have constraints on the affine transformation
using
its orthogonality, we have constraints on the affine transformation
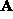 called metric constraints:
called metric constraints:
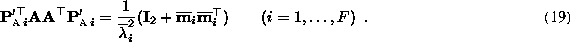
Let  and
and 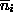 be two elements of
be two elements of
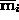 . Then, eliminating
. Then, eliminating
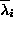 from
(19), we obtain
from
(19), we obtain
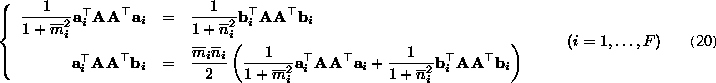
which gives 2F linear homogeneous equations in terms of 6 elements of
the 3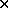 3 symmetric matrix
3 symmetric matrix 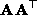 . If three or
more views are available, we can obtain a least-squares solution
determined up to a scale as a solution of the ordinary eigenvalue
problem. Once
. If three or
more views are available, we can obtain a least-squares solution
determined up to a scale as a solution of the ordinary eigenvalue
problem. Once 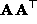 is determined,
is determined, 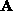 is
recovered through, for instance, Cholesky decomposition.
is
recovered through, for instance, Cholesky decomposition.
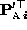 be an affine camera motion
obtained by factoring the measurement matrix. Then
be an affine camera motion
obtained by factoring the measurement matrix. Then
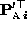 is related to the ``true'' motion
is related to the ``true'' motion
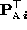 described with respect to the
Euclidean coordinate frame by (9). Our goal here
is to obtain the affine transformation
described with respect to the
Euclidean coordinate frame by (9). Our goal here
is to obtain the affine transformation  (up to an arbitrary
rotation) in (9) with which affine descriptions
(up to an arbitrary
rotation) in (9) with which affine descriptions
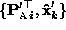 of
motion and shape are corrected to Euclidean ones
of
motion and shape are corrected to Euclidean ones
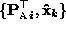 .
.



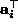 and
and 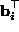 denote two rows of
denote two rows of
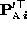 . Then, for each affine camera
model introduced in §
. Then, for each affine camera
model introduced in §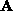 is determined as follows;
is determined as follows;
 using
its orthogonality, we have constraints on the affine transformation
using
its orthogonality, we have constraints on the affine transformation
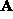 called metric constraints:
called metric constraints:
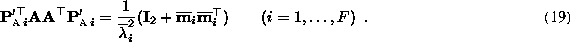
 and
and 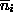 be two elements of
be two elements of
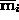 . Then, eliminating
. Then, eliminating
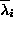 from
(
from
(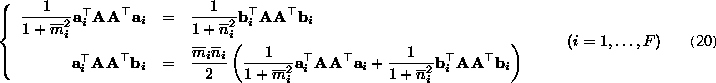
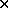 3 symmetric matrix
3 symmetric matrix 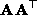 . If three or
more views are available, we can obtain a least-squares solution
determined up to a scale as a solution of the ordinary eigenvalue
problem. Once
. If three or
more views are available, we can obtain a least-squares solution
determined up to a scale as a solution of the ordinary eigenvalue
problem. Once 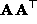 is determined,
is determined, 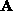 is
recovered through, for instance, Cholesky decomposition.
is
recovered through, for instance, Cholesky decomposition.
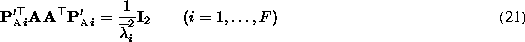
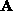 is determined as a
least-squares solution of the following equations:
is determined as a
least-squares solution of the following equations:


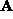 is recovered by solving, in the
least-squares sense,
is recovered by solving, in the
least-squares sense,
