The Process to be Estimated
As described above in
section
, the Kalman filter addresses the general problem of trying to estimate the state 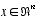 of a discrete-time controlled process that is governed by a linear stochastic difference equation. But what happens if the process to be estimated and (or) the measurement relationship to the process is non-linear? Some of the most interesting and successful applications of Kalman filtering have been such situations. A Kalman filter that linearizes about the current mean and covariance is referred to as an extended Kalman filter or EKF
.
of a discrete-time controlled process that is governed by a linear stochastic difference equation. But what happens if the process to be estimated and (or) the measurement relationship to the process is non-linear? Some of the most interesting and successful applications of Kalman filtering have been such situations. A Kalman filter that linearizes about the current mean and covariance is referred to as an extended Kalman filter or EKF
.
In something akin to a Taylor series, we can linearize the estimation around the current estimate using the partial derivatives of the process and measurement functions to compute estimates even in the face of non-linear relationships. To do so, we must begin by modifying some of the material presented in
section
. Let us assume that our process again has a state vector 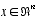 , but that the process is now governed by the non-linear stochastic difference equation
, but that the process is now governed by the non-linear stochastic difference equation
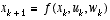 , (2.1)
, (2.1)
with a measurement 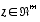 that is
that is
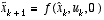 (2.3)
(2.3)
and
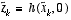 , (2.4)
, (2.4)
where 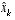 is some a posteriori estimate of the state (from a previous time step k).
is some a posteriori estimate of the state (from a previous time step k).
The Computational Origins of the Filter
To estimate a process with non-linear difference and measurement relationships, we begin by writing new governing equations that linearize an estimate about
(2.3)
and
(2.4)
,
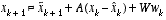 , (2.5)
, (2.5)
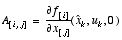 ,
,
-
W is the Jacobian matrix of partial derivatives of f(·) with respect to w,
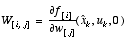 ,
,
-
H is the Jacobian matrix of partial derivatives of h(·) with respect to x,
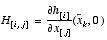 ,
,
-
V is the Jacobian matrix of partial derivatives of h(·) with respect to v,
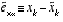 , (2.7)
, (2.7)
and the measurement residual,
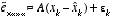 , (2.9)
, (2.9)
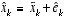 . (2.11)
. (2.11)
The random variables of
(2.9)
and
(2.10)
have approximately the following probability distributions (see the previous footnote):
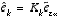 . (2.12)
. (2.12)
By substituting
(2.12)
back into
(2.11)
and making use of
(2.8)
we see that we do not actually need the second (hypothetical) Kalman filter:
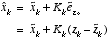 (2.13)
(2.13)
Equation
(2.13)
can now be used for the measurement update in the extended Kalman filter, with 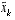 and
and 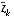 coming from
(2.3)
and
(2.4)
, and the Kalman gain
coming from
(2.3)
and
(2.4)
, and the Kalman gain 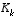 coming from
(1.11)
with the appropriate substitution for the measurement error covariance.
coming from
(1.11)
with the appropriate substitution for the measurement error covariance.
The complete set of EKF equations is shown below in
Table 2-1
and
Table 2-2
. Note that we have substituted 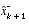 for
for 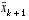 to remain consistent with the earlier "super minus" notation, and that we now attach the subscript
to remain consistent with the earlier "super minus" notation, and that we now attach the subscript 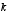 to the Jacobians
to the Jacobians 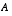 ,
, 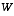 ,
, 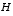 , and
, and 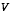 , to reinforce the notion that they are different at (and therefore must be recomputed at) each time step.
, to reinforce the notion that they are different at (and therefore must be recomputed at) each time step.
Table 2-1:
EKF time update equations.
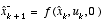 (2.14)
(2.14)
|
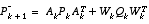 (2.15)
(2.15)
|
As with the basic discrete Kalman filter, the time update equations in
Table 2-1
project the state and covariance estimates from time step k to step k+1. Again f(·) in
(2.14)
comes from
(2.3)
, 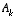 and W are the process Jacobians at step k, and
and W are the process Jacobians at step k, and 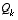 is the process noise covariance
(1.3)
at step k.
is the process noise covariance
(1.3)
at step k.
Table 2-2:
EKF measurement update equations.
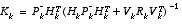 (2.16)
(2.16)
|
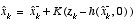 (2.17)
(2.17)
|
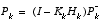 (2.18)
(2.18)
|
As with the basic discrete Kalman filter, the measurement update equations in
Table 2-2
correct the state and covariance estimates with the measurement 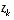 . Again h(·) in
(2.17)
comes from
(2.4)
,
. Again h(·) in
(2.17)
comes from
(2.4)
, 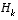 and V are the measurement Jacobians at step k, and
and V are the measurement Jacobians at step k, and 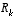 is the measurement noise covariance
(1.4)
at step k.
[CVonline Ed. note:
While I'm not a KF expert, the Measurement Update equations seem
to have incremented the time variable t, so t in the Measurement Update equations is the
same as t+1 in the Time Update equations.]
is the measurement noise covariance
(1.4)
at step k.
[CVonline Ed. note:
While I'm not a KF expert, the Measurement Update equations seem
to have incremented the time variable t, so t in the Measurement Update equations is the
same as t+1 in the Time Update equations.]
The basic operation of the EKF is the same as the linear discrete Kalman filter as shown in
Figure 1-1
.
Figure 2-1
below offers a complete picture of the operation of the EKF, combining the high-level diagram of
Figure 1-1
with the equations from
Table 2-1
and
Table 2-2
.
Figure 2-1.
A complete picture of the operation of the extended Kalman filter, combining the high-level diagram of Figure 1-1
with the equations from Table 2-1
and Table 2-2
.
An important feature of the EKF is that the Jacobian 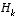 in the equation for the Kalman gain
in the equation for the Kalman gain 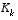 serves to correctly propagate or "magnify" only the relevant component of the measurement information. For example, if there is not a one-to-one mapping between the measurement
serves to correctly propagate or "magnify" only the relevant component of the measurement information. For example, if there is not a one-to-one mapping between the measurement 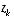 and the state via h(·), the Jacobian
and the state via h(·), the Jacobian 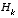 affects the Kalman gain so that it only magnifies the portion of the residual
affects the Kalman gain so that it only magnifies the portion of the residual 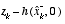 that does affect the state. Of course if over all measurements there is not a one-to-one mapping between the measurement
that does affect the state. Of course if over all measurements there is not a one-to-one mapping between the measurement 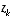 and the state via h(·), then as you might expect the filter will quickly diverge. The control theory term to describe this situation is unobservable.
and the state via h(·), then as you might expect the filter will quickly diverge. The control theory term to describe this situation is unobservable.
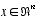 of a discrete-time controlled process that is governed by a linear stochastic difference equation. But what happens if the process to be estimated and (or) the measurement relationship to the process is non-linear? Some of the most interesting and successful applications of Kalman filtering have been such situations. A Kalman filter that linearizes about the current mean and covariance is referred to as an extended Kalman filter or EKF
1
.
of a discrete-time controlled process that is governed by a linear stochastic difference equation. But what happens if the process to be estimated and (or) the measurement relationship to the process is non-linear? Some of the most interesting and successful applications of Kalman filtering have been such situations. A Kalman filter that linearizes about the current mean and covariance is referred to as an extended Kalman filter or EKF
1
.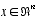 , but that the process is now governed by the non-linear stochastic difference equation
, but that the process is now governed by the non-linear stochastic difference equation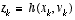 , (2.2)
, (2.2)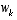 and
and 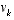 again represent the process and measurement noise as in
(1.3)
and
(1.4)
. In this case the non-linear function f(·) in the difference equation
(2.1)
relates the state at time step k to the state at step k+1. It includes as parameters any driving function uk and the zero-mean process noise wk. The non-linear function h(·) in the measurement equation
(2.2)
relates the state
again represent the process and measurement noise as in
(1.3)
and
(1.4)
. In this case the non-linear function f(·) in the difference equation
(2.1)
relates the state at time step k to the state at step k+1. It includes as parameters any driving function uk and the zero-mean process noise wk. The non-linear function h(·) in the measurement equation
(2.2)
relates the state 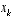 to the measurement
to the measurement 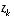 .
.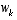 and
and 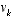 at each time step. However, one can approximate the state and measurement vector without them as
at each time step. However, one can approximate the state and measurement vector without them as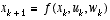 , (2.1)
, (2.1)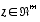 that is
that is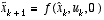 (2.3)
(2.3)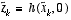 , (2.4)
, (2.4)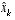 is some a posteriori estimate of the state (from a previous time step k).
is some a posteriori estimate of the state (from a previous time step k).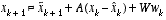 , (2.5)
, (2.5)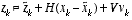 . (2.6)
. (2.6)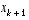 and
and 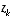 are the actual state and measurement vectors,
are the actual state and measurement vectors,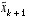 and
and 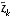 are the approximate state and measurement vectors from
are the approximate state and measurement vectors from 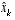 is an a posteriori estimate of the state at step k,
is an a posteriori estimate of the state at step k,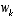 and
and 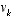 represent the process and measurement noise as in
represent the process and measurement noise as in 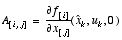 ,
,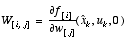 ,
,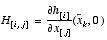 ,
,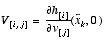 .
.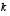 with the Jacobians
with the Jacobians 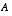 ,
, 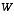 ,
, 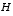 , and
, and 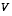 , even though they are in fact different at each time step.
, even though they are in fact different at each time step.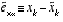 , (2.7)
, (2.7)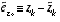 . (2.8)
. (2.8)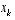 in
in 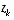 in
in 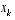 . Using
. Using 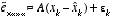 , (2.9)
, (2.9)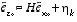 , (2.10)
, (2.10)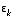 and
and 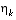 represent new independent random variables having zero mean and covariance matrices
represent new independent random variables having zero mean and covariance matrices 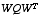 and
and 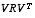 , with
, with 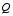 and
and 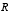 as in
as in 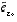 in
in 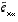 given by
given by 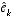 , could then be used along with
, could then be used along with 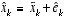 . (2.11)
. (2.11)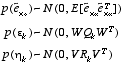
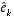 be zero, the Kalman filter equation used to estimate
be zero, the Kalman filter equation used to estimate 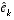 is
is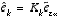 . (2.12)
. (2.12)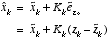 (2.13)
(2.13)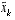 and
and 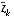 coming from
coming from 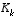 coming from
coming from 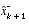 for
for 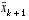 to remain consistent with the earlier "super minus" notation, and that we now attach the subscript
to remain consistent with the earlier "super minus" notation, and that we now attach the subscript 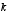 to the Jacobians
to the Jacobians 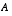 ,
, 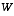 ,
, 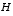 , and
, and 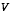 , to reinforce the notion that they are different at (and therefore must be recomputed at) each time step.
, to reinforce the notion that they are different at (and therefore must be recomputed at) each time step. 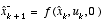 (2.14)
(2.14)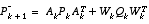 (2.15)
(2.15)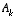 and W are the process Jacobians at step k, and
and W are the process Jacobians at step k, and 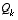 is the process noise covariance
is the process noise covariance 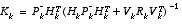 (2.16)
(2.16)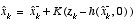 (2.17)
(2.17)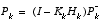 (2.18)
(2.18)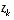 . Again h(·) in
. Again h(·) in 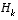 and V are the measurement Jacobians at step k, and
and V are the measurement Jacobians at step k, and 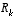 is the measurement noise covariance
is the measurement noise covariance 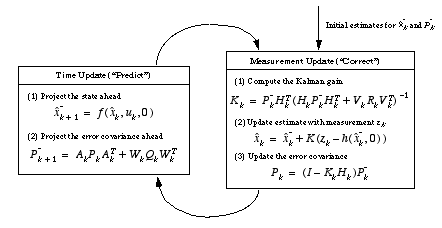
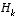 in the equation for the Kalman gain
in the equation for the Kalman gain 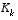 serves to correctly propagate or "magnify" only the relevant component of the measurement information. For example, if there is not a one-to-one mapping between the measurement
serves to correctly propagate or "magnify" only the relevant component of the measurement information. For example, if there is not a one-to-one mapping between the measurement 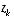 and the state via h(·), the Jacobian
and the state via h(·), the Jacobian 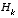 affects the Kalman gain so that it only magnifies the portion of the residual
affects the Kalman gain so that it only magnifies the portion of the residual 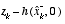 that does affect the state. Of course if over all measurements there is not a one-to-one mapping between the measurement
that does affect the state. Of course if over all measurements there is not a one-to-one mapping between the measurement 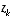 and the state via h(·), then as you might expect the filter will quickly diverge. The control theory term to describe this situation is unobservable.
and the state via h(·), then as you might expect the filter will quickly diverge. The control theory term to describe this situation is unobservable.