The
Sobel operator performs a 2-D spatial gradient
measurement on an image and so emphasizes regions of
high spatial frequency
that correspond to edges. Typically it is used to find the
approximate absolute gradient magnitude at each point in an input
grayscale image.
In theory at least, the operator consists of a pair of 3×3 convolution kernels as shown in Figure 1. One kernel is simply the other rotated by 90°. This is very similar to the Roberts Cross operator.
Figure 1 Sobel convolution kernels
These kernels are designed to respond maximally to edges running vertically and horizontally relative to the pixel grid, one kernel for each of the two perpendicular orientations. The kernels can be applied separately to the input image, to produce separate measurements of the gradient component in each orientation (call these Gx and Gy). These can then be combined together to find the absolute magnitude of the gradient at each point and the orientation of that gradient. The gradient magnitude is given by:
Typically, an approximate magnitude is computed using: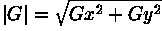
which is much faster to compute.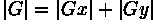
The angle of orientation of the edge (relative to the pixel grid) giving rise to the spatial gradient is given by:
In this case, orientation 0 is taken to mean that the direction of maximum contrast from black to white runs from left to right on the image, and other angles are measured anti-clockwise from this.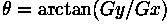
Often, this absolute magnitude is the only output the user sees --- the two components of the gradient are conveniently computed and added in a single pass over the input image using the pseudo-convolution operator shown in Figure 2.
Figure 2 Pseudo-convolution kernels used to quickly compute approximate gradient magnitude
Using this kernel the approximate magnitude is given by:
The Sobel operator is slower to compute than the Roberts Cross operator, but its larger convolution kernel smooths the input image to a greater extent and so makes the operator less sensitive to noise. The operator also generally produces considerably higher output values for similar edges, compared with the Roberts Cross.
As with the Roberts Cross operator, output values from the operator can easily overflow the maximum allowed pixel value for image types that only support smallish integer pixel values (e.g. 8-bit integer images). When this happens the standard practice is to simply set overflowing output pixels to the maximum allowed value. The problem can be avoided by using an image type that supports pixel values with a larger range.
Natural edges in images often lead to lines in the output image that are several pixels wide due to the smoothing effect of the Sobel operator. Some thinning may be desirable to counter this. Failing that, some sort of hysteresis ridge tracking could be used as in the Canny operator.
The image
shows the results of applying the Sobel operator to
Compare this with the equivalent Roberts Cross output
Note that the spurious noise that afflicted the Roberts Cross output image is still present in this image, but its intensity relative to the genuine lines has been reduced, and so there is a good chance that we can get rid of this entirely by thresholding. Also, notice that the lines corresponding to edges have become thicker compared with the Roberts Cross output due to the increased smoothing of the Sobel operator.
The image
shows a simpler scene containing just a single flat dark object against a lighter background. Applying the Sobel operator produces
Note that the lighting has been carefully set up to ensure that the edges of the object are nice and sharp and free of shadows.
The Sobel edge detector can also be applied to
range images
like
The corresponding edge image is
All edges in the image have been detected and can be nicely separated from the background using a threshold of 150, as can be seen in
Although the Sobel operator is not as sensitive to noise as the Roberts Cross operator, it still amplifies high frequencies. The image
is the result of adding Gaussian noise with a standard deviation of 15 to the original image. Applying the Sobel operator yields
and thresholding the result at a value of 150 produces
We can see that the noise has increased during the edge detection and it is no longer possible to find a threshold which removes all noise pixels and at the same time retains the edges of the objects.
The object in the previous example contains sharp edges and its surface is rather smooth. Therefore, we could (in the noise-free case) easily detect the boundary of the object without getting any erroneous pixels. A more difficult task is to detect the boundary of
because it contains many fine depth variations (i.e. resulting in intensity changes in the image) on its surface. Applying the Sobel operator straightforwardly yields
We can see that the intensity of many pixels on the surface is as high as along the actual edges. One reason is that the output of many edge pixels is greater than the maximum pixel value and therefore they are `cut off' at 255. To avoid this overflow we scale the range image by a factor 0.25 prior to the edge detection and then normalize the output, as can be seen in
Although the result has improved significantly, we still cannot find a threshold so that a closed line along the boundary remains and all the noise disappears. Compare this image with the results obtained with the Canny edge detector.
A related operator is the Prewitt gradient edge detector (not to be confused with the Prewitt compass edge detector). This works in a very similar way to the Sobel operator but uses slightly different kernels, as shown in Figure 3. This kernel produces similar results to the Sobel, but is not as isotropic in its response.
Figure 3 Masks for the Prewitt gradient edge detector.
You can interactively experiment with this operator by clicking here.
and see if you can use thresholding to detect the edges of the object without also selecting noisy pixels. Compare the results with those obtained with the Roberts Cross operator.
R. Gonzalez and R. Woods Digital Image Processing, Addison Wesley, 1992, pp 414 - 428.
R. Boyle and R. Thomas Computer Vision: A First Course, Blackwell Scientific Publications, 1988, pp 48 - 50.
E. Davies Machine Vision: Theory, Algorithms and Practicalities, Academic Press, 1990, Chap. 5.
D. Vernon Machine Vision, Prentice-Hall, 1991, Chap. 5.
Specific information about this operator may be found here.
More general advice about the local HIPR installation is available in the Local Information introductory section.
©2003 R. Fisher, S. Perkins,
A. Walker and E. Wolfart.
