Matrix inversion
The great difficulty with Gaussian process methods comes from the need to invert large covariance matrices. Standard inversion techniques scale as the cube of n where the matrix is of size n by n.
There are methods of approximating this inversion more efficiently. However if the matrix takes a Toeplitz form, then inversion is much faster. Exact inversion can be achieved at a scaling of the square of n using the Trench algorithm, approximate inversion at nlogn.
What does the Toeplitz form look like? A matrix where every element on each diagonal is identical is Toeplitz. Such matrices would be generated from regular samples in 1D from a process with a stationary covariance function. Unfortunately when the dimensionality of the space is greater than one we no longer get Toeplitz structures. In fact we get block-Toeplitz Toeplitz-block (BTTB) structures, such as that illustrated below (illustration by Kees Hindriks, included with permission).
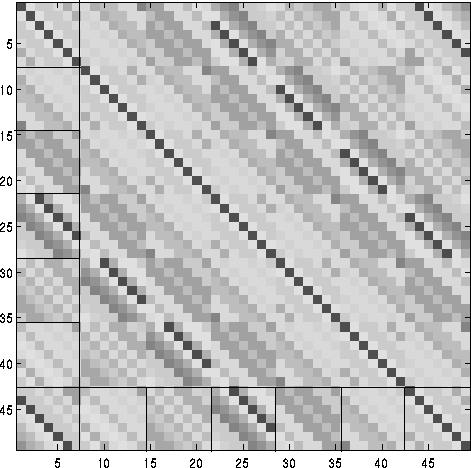
Unfortunately the Trench algorithm cannot be used to invert BTTB matrices.
There is a way of approximating the covariance matrix by a Toeplitz one. If covariance functions of finite support are used, then the covariance terms between points greater than a certain distance apart is zero. This enables us to warp our space without seriously affecting the covaraince we obtain, so long as the local metric is relatively undisturbed. If we wrap our space around a cylinder, and then sample from a spiral around that cylinder, we can once again obtain a Toeplitz matrix.