Geometry Explorer: Combining Dynamic Geometry, Automated Geometry Theorem Proving and Diagrammatic Proofs
Introduction
Our Geometry Explorer system integrates a dynamic geometry interface with an automated geometry theorem prover. This can be used to explore geometry diagrams, automatically prove theorems about them and produce novel diagrammatic proofs.
Dynamic Geometry
Dynamic geometry software allows users to create Euclidean geometry diagrams using ruler and compass construction tools, in a similar way to how they are sketched on paper. Constructions can then be moved and dependent construction positions will update automatically, creating new diagram instances. This allows exploration of known diagram properties and can help users to nd new conjectures in ways not possible with static diagrams.
Example (Nine Point Circle Theorem): Let AD be the altitude on BC and let the midpoints of the sides AB, BC and CA of 4ABC be E, F and G respectively. Show that D, E, F and G are cyclic.
The hypotheses of the example can be constructed and explored using the Geometry Explorer GUI:
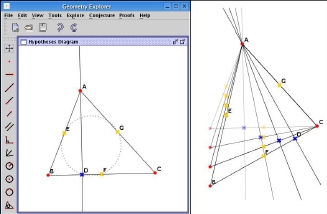
Fig. 1. The Geometry Explorer GUI (left) and exploring dynamic diagram instances (right).
After the user specifies the conjecture for the example theorem, the integrated full-angle method theorem prover automatically generates a proof.
The Full-Angle Method
The full-angle method can automatically generate short and human-readable theorem proofs, making use of a geometric invariant called the full-angle.
Full-angles: The full-angle between lines u and v is denoted as <[u, v] and is the rotation required to make u to be parallel to v. We use the constants <[0] and <[1] such that:
- <[u, v] = <[0] if u || v,
- <[u, v] = <[1] if u ⊥ v, and
- <[1] + <[1] = <[0].
The following steps are used to fi nd a theorem proof:
- In predicate form, the hypotheses is put into what is called the Geometry Information Basis (GIB).
- Exhaustive forward-chaining is applied to the GIB to discover new facts, using rules such as:
- F3 If M and N are the midpoints of AB and AC respectively then MN || BC.
- F5 If O is the midpoint of CA and AB ⊥ BC then O is the circumcentre of ΔABC.
- The theorem conjecture is represented as <[0] = Σfi, where fi is a full-angle.
- Full-angles are replaced with equal expressions using conditional rewrite rules such as:
- R1 <[AB,CD] = <[AB,EF] if CD || EF.
- R2 <[AB,CD] = <[AB,EF] + <[1] if CD ⊥ EF.
- R6 <[AB,BC] = <[AD,CD] if A, B, C, and D are cyclic.
- A search algorithm is used to fi nd a sequence of rewrites that transforms the full-angle equation to <[0] = <[0], giving a backward-chaining proof.
Diagrammatic Proofs
Geometry Explorer can visualise full-angle method proofs diagrammatically. Forward-chaining reasoning is shown as a graph, where nodes represent known geometry facts. Edges show which facts inferred others, with labels showing the rule used:
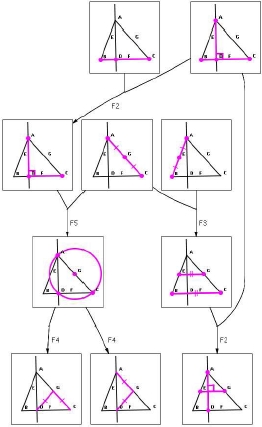
Fig. 2. A diagrammatic forward-chaining proof of some interesting discovered facts.
The user can then explore discovered facts by manipulating the dynamic diagram:
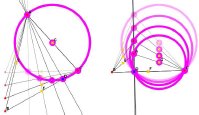
Fig. 3. Exploring a discovered circumcircle.
The backward-chaining proof is shown as a graph where each node represents a full-angle. Full-angles x and y joined to z with a “+” node means that x+y = z. Using rule R6, the example theorem conjecture is represented as <[0] = <[EF, FD] + <[DG, GE], as shown at the top of the graph. Edges labelled with rule names show rewrite rule applications and the cancellations at the bottom complete the proof:
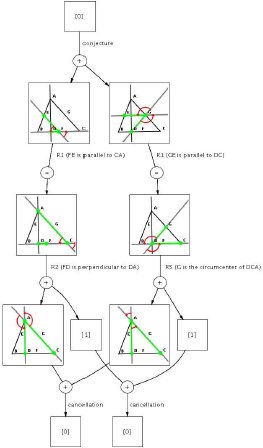
Fig. 4. A diagrammatic backward-chaining proof showing that D, E, F, and G are cyclic.
Publications
- Wilson, S. and Fleuriot, J. D. (2005). Combining dynamic geometry, automated geometry theorem proving and diagrammatic proofs. In Proceedings of the User Interfaces for Theorem Provers Workshop.
- Wilson, S. and Fleuriot, J. D. Geometry Explorer: Combining dynamic geometry, automated geometry theorem proving and diagrammatic proofs. To appear in: Electronic Notes in Theoretical Computer Science (In Limbo: Camera ready version submitted but awaiting to be published as a UITP special issue since 2006!).

