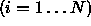Suppose we have a set of N points 
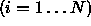and we
wish to find the `best' straight line through them. To define `best' we need
to give a quality of fit measure. Let us first choose an appropriate
parameterization of the line;
where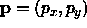 
is the closest approach of the line to the origin and
thus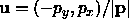 
is normal to the vector p.
We choose this form as it gives both parameters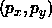 
the same units.
It is simple to show that the normal distance of such a line to a point
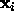is given by
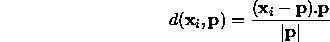
If we assume a density distribution for this distance,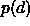 
, and that
the points are independent samples from a distribution about the true
line, we can construct a log likelihood function (see above)
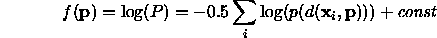
which must be maximized.
If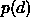 
is gaussian the problem can be solved by taking the line through
the centroid of the N points parallel to the principle eigenvector of the
covariance matrix of the data about the centroid. If, however, a non-gaussian distribution
is used, we revert to using the optimization methods described above to
choose the parameters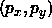 
which maximize 
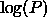. Typically
we would use a local optimizer, obtaining a starting point by first solving
with an assumed gaussian form for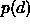 
. If the function 
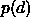is twice differentiable then 
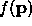is twice differentiable, and the
Levenberg-Marquardt method can be used.
For instance, robust line fitting techniques accommodate outliers by
assuming a distribution for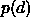 
with longer tails than the gaussian
[6]. For instance
or a gaussian with extended tails
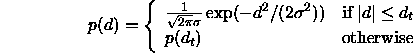
Note that this latter is not strictly a probability density distribution
since it does not have unit area, but this does not affect the parameter
estimation. Note also that the latter is not differentiable at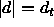 
,
so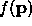 
can only be optimized using a method which does not
require derivatives, such as Simplex or Powell's.
In any parameter estimation problem it is important to estimate the
confidence region about the parameter estimates obtained.
If 
is gaussian then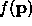 
is a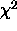 
function. The
found parameters can be considered to be drawn from a multivariate
normal distribution about 
(which achieve the optimum)
with a covariance matrix given by the inverse of the Hessian of f
evaluated at 
. Confidence ellipsoids about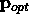 
can be drawn up at suitable levels using this covariance matrix [6].
If 
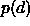is not gaussian then more detailed analytic calculations or
a Monte Carlo simulation are required to obtain the confidence limits.
The approach given above makes the assumption that measurement errors in the data points are equal in all directions. If this is not the case the merit function must be reformulated accordingly.