



Next: Fitting Parameterized Models
Up: Curve Fitting
Previous: Fitting Straight Lines
The line 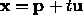 is a special case of the general parametric curve
is a special case of the general parametric curve 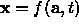 , where t moves x along the curve defined by
parameters a. Finding the parameters, a, which best
fit such a general curve
through a set of 2D data points can be complicated because of the
difficulty of defining and evaluating a suitable likelihood function.
Simply calculating the closest approach distance of the curve to a
single data point
, where t moves x along the curve defined by
parameters a. Finding the parameters, a, which best
fit such a general curve
through a set of 2D data points can be complicated because of the
difficulty of defining and evaluating a suitable likelihood function.
Simply calculating the closest approach distance of the curve to a
single data point 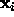 requires a minimization in itself
(ie Find t which minimizes
requires a minimization in itself
(ie Find t which minimizes 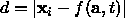 ).
This leads to nasty nested minimization problems of the form
).
This leads to nasty nested minimization problems of the form
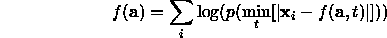
A special case worth describing is when the curve can be written in
the form
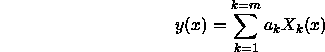
where  are arbitrary fixed functions of x called basis
functions. The only unknown parameters are the m weights
are arbitrary fixed functions of x called basis
functions. The only unknown parameters are the m weights 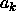 .
If we wish to find the best fit of such a function to N points
.
If we wish to find the best fit of such a function to N points 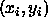 where the
where the 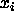 are known precisely but the
are known precisely but the 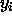 have a gaussian
measurement error with standard deviation of
have a gaussian
measurement error with standard deviation of 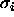 , we can use
and approach called General Least Squares.
We define a log-likelihood function
, we can use
and approach called General Least Squares.
We define a log-likelihood function
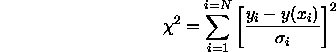
The parameters a which minimize this can be found as follows.
Define an N x m design matrix D such that

Define an N element vector r such that

It can be shown [6] that the optimal choice of parameters
is given by using a singular value decomposition to give the least
squares solution to the linear equation

If D is decomposed as 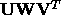 with
V m x m and orthonormal, then the covariance of the estimate
of parameters a is given by
with
V m x m and orthonormal, then the covariance of the estimate
of parameters a is given by 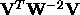 .
.
Bob Fisher
Fri Mar 28 14:12:50 GMT 1997
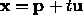 is a special case of the general parametric curve
is a special case of the general parametric curve 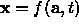 , where t moves x along the curve defined by
parameters a. Finding the parameters, a, which best
fit such a general curve
through a set of 2D data points can be complicated because of the
difficulty of defining and evaluating a suitable likelihood function.
Simply calculating the closest approach distance of the curve to a
single data point
, where t moves x along the curve defined by
parameters a. Finding the parameters, a, which best
fit such a general curve
through a set of 2D data points can be complicated because of the
difficulty of defining and evaluating a suitable likelihood function.
Simply calculating the closest approach distance of the curve to a
single data point 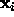 requires a minimization in itself
(ie Find t which minimizes
requires a minimization in itself
(ie Find t which minimizes 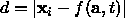 ).
This leads to nasty nested minimization problems of the form
).
This leads to nasty nested minimization problems of the form




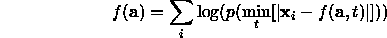
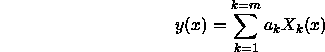
 are arbitrary fixed functions of x called basis
functions. The only unknown parameters are the m weights
are arbitrary fixed functions of x called basis
functions. The only unknown parameters are the m weights 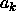 .
If we wish to find the best fit of such a function to N points
.
If we wish to find the best fit of such a function to N points 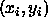 where the
where the 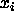 are known precisely but the
are known precisely but the 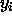 have a gaussian
measurement error with standard deviation of
have a gaussian
measurement error with standard deviation of 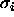 , we can use
and approach called General Least Squares.
We define a log-likelihood function
, we can use
and approach called General Least Squares.
We define a log-likelihood function
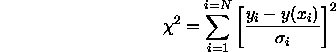



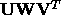 with
V m x m and orthonormal, then the covariance of the estimate
of parameters a is given by
with
V m x m and orthonormal, then the covariance of the estimate
of parameters a is given by 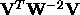 .
.