Notice that the equations written to this point are sufficient to guarantee rectification: to prove this, let us verify that epipolar lines are parallel and horizontal.
When 
(the epipole is at infinity) the
epipolar lines are parallel to the vector 
As we know, each epipole is the projection of the
conjugate optical centre, i.e.
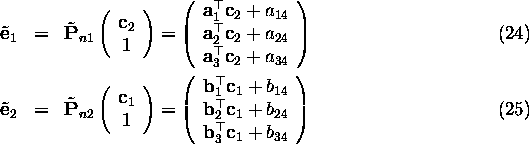
Hence epipolar lines are are horizontal when:
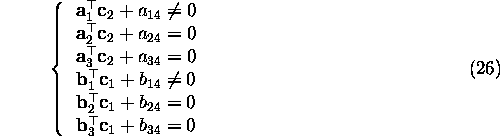
The four equations are satisfied as long as Equations (19), (18) and (23) hold, as one can easily verify.
Although rectification is guaranteed, the orientation of the retinal plane has still one degree of freedom. Moreover, the constraints written up to now are not enough to obtain a unique PPM. We shall therefore choose explicitly the intrinsic parameters to obtain enough equations.