Now that - for each camera - the rectifying PPM is known, we want to
compute the linear transformation (in projective coordinates) that
maps the retinal plane of the old PPM, 
, onto the retinal plane of 
.
We will see that this transformation
is the 
matrix 
.
For any 3-D point w we can write
We know from Eq. (10) that the equation of the optical ray
associated to 
is
hence
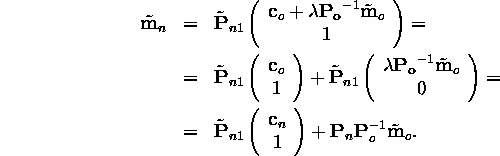
Assuming that rectification does not alter the optical centre ( 
), we obtain:
The transformation 
is then applied to the original image to
produce a rectified image, as in Fig. 3. Note that the
pixels (integer-coordinate positions) of the rectified image
correspond, in general, to non-integer positions on the original image
plane. Therefore, the gray levels of the rectified image are computed
by bilinear interpolation.