Coherence Based Stereo
The estimation of disparity shares many similarities with the computation of optical flow. But having available only two discrete ``time''-samples, namely the images of the left and right view, creates an additional problem in disparity estimation. The discrete sampling of visual space leads to aliasing effects which limit the working ranges of simple disparity detectors.
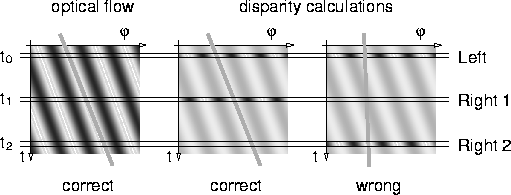
Figure 1: The velocity of an image patch manifests itself as the main texture direction in the space-time flow field traced out by the intensity pattern in time (left). Sampling such flow patterns at discrete time points can create aliasing effects which lead to wrong estimates if the velocity of the flow is too fast (right). Using optical flow estimation techniques for disparity calculations, this problem is always present, since only the two samples obtained from the left and right eye are available for flow estimation.
For an explanation consider Figure 1. If a small surface patch is shifted over time, the intensity pattern of the patch traces out a corresponding flow pattern in spacetime. The principal texture direction of this flow pattern indicates the velocity of the image patch. It can be estimated without difficulty if the intensity data for all time points is available (Fig. 1, left). Even if the flow pattern can not be sampled continuously, but only at some discrete time points, the shift can be estimated without ambiguity if this shift is not too large (Fig. 1, middle). However, if the shift between the two samples exceeds a certain limit, this becomes impossible (Fig. 1, right). The wrong estimates are caused by simple aliasing in the ``time''-direction; an everday example of this effect is sometimes seen as motion reversal in movies.
To formalize, let 
be the image intensity of a small patch in the left view of a scene with
corresponding Fourier transform 
. Moving the left camera on a linear path to the position of the right
camera, we obtain a local flow-field very similar to Figure 1,
namely: 
. Here 
is the disparity of the image patch and the shift parameter 
runs from 0 to 1. The Fourier transform of 
follows from elementary calculus as 
. Now, if the spectrum of
is bounded by some maximum wavevector 
, i.e. if 
for 
, we find as highest wavevector of the flow field 
in
-direction 
. However, the maximal representable wavevector in this direction is given
by sampling theory as 
. Since sampling in
-direction is done with a step size of 
, we obtain as an upper bound for sampling the flow field without aliasing
effects
Equation (1) states that
the range of reliable disparities estimates for a simple detector is limited
by the largest wavevector present in the image data. This size-disparity
scaling is well-known in the context of spatial frequency channels assumed
to exist in the visual cortex. Cortical cells respond to spatial frequencies
up to about twice their peak wavelength 
, therefore limiting the range of detectable disparities to values less
than 
. This is known as Marr's quarter-cycle limit [8,
9].
Since image data is usually sampled in spatial direction with some fixed
receptor spacing 
, the highest wavevector
which can be present in the data after retinal sampling is given by 
. This leads to the requirement that 
-- without additional processing steps, only disparities less than
the receptor spacing can be estimated reliably by a simple disparity
unit.
Equation (1) immediately
suggests a way to extend the aliasing limited working range of disparity
detectors: spatial prefiltering of the image data before or during disparity
calculation reduces
, and in turn increases the disparity range. In this way, larger disparities
can be estimated, but only with the consequence of reducing simultaneously
the spatial resolution of the resulting disparity map.
Another way of modifying the disparity range is the application of a preshift to the input data of the detectors before the disparity calculation. However, modification of the disparity range by preshifting requires prior knowledge of the correct preshift to be applied, which is a nontrivial problem. One could resort again to hierarchical coarse-to-fine schemes by using disparity estimates obtained at some coarse spatial scale to adjust the processing at finer spatial scales, but the drawbacks inherent to hierarchical schemes have already been elaborated.
Instead of counteracting the aliasing effects discussed, one can utilize
them within a new computational paradigm. Basic to the new approach is
a stack of simple disparity estimators, all responding to a common view
direction, with each unit 
having some preshift or presmoothing applied to its input data. Such a
stack might even be composed of different types of disparity units. Due
to random preshifts and presmoothing, the units within the stack will have
different and slightly overlapping working ranges of reliable disparity
estimates, 
.
If an object seen in the common view direction of the stack has true
disparity
, the stack will be split by the stimulus into two disjunct classes: the
class 
of detectors with 
for all 
, and the rest of the stack, 
, where 
. All disparity detectors 
will code more or less the true disparity 
, but the estimates of detectors belonging to
will be subject to random aliasing effects, depending in a complicated
way on image content and specific disparity ranges 
of the units. Thus, we will have 
whenever units
and 
belong to
, and random values otherwise. A simple coherence detection within each
stack, i.e. searching for all units with 
and extracting the largest cluster found will be sufficient to single out
. The true disparity
in the common view direction of the stack can be estimated as an average
over the detected cluster:
The coherence detecting scheme has to be repeated for every view direction and leads to a fully parallel algorithm for disparity calculation. Neighboring disparity stacks responding to different view directions estimate disparity independently from each other.
Since coherence detection is based on analyzing the multi-unit activity within a stack, the scheme turns out to be extremely robust against single-unit failure. As long as the density of disparity estimators remains high enough along a specific view direction, no substantial loss of network performance will be noticed.
| Prev: Introduction | Up: ^ Table of Contents ^ | Next: Computational Structure |
Comments are welcome! © 1997 by Rolf Henkel - all rights reserved.