Computational Structure
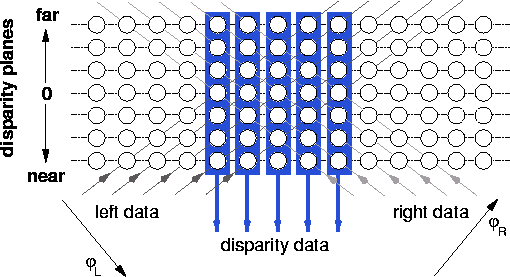
A computational structure realizing coherence-based stereo is quite simple (Figure 2). Arranging identical disparity units into horizontal disparity layers, left and right image data is fed into the network of disparity layers along diagonally running data lines. Thus each disparity layer receives the stereo data with a certain fixed preshift applied. This varying preshift between disparity layers leads to slightly different working-ranges of neighboring layers. Disparity units stacked vertically above each other are collected into the disparity stacks which are analyzed for coherently coding subpopulations of disparity units.
Figure 2: The network structure for calculating stereo by coherence detection. Simple disparity estimators are arranged in horizontal layers, which have slightly overlapping working ranges. Image data is fed into the network along diagonal running data lines. Within each of the vertical disparity stacks, coherently coding subpopulations of disparity units are detected, and the average disparity value of these pools is finally read out by the mechanism.
In most of the simulations reported below, responses of two disparity
units 
and 
in a given stack are marked as coherent with each other whenever 
. Only the largest cluster found in each stack is read out by the coherence
mechanism.
This type of coherence detection can be realized easily with biological hardware, for example with neuronally implemented limit-cycle oscillators [10]. Assuming appropriate links structures, these neural oscillators will synchronize their responses, but only if they code approximately the same stimulus value [11]. A valid disparity estimate would show up in such a network as a strong coherent neuronal signal.
For the disparity estimators, various circuitry can be used. In the simulations reported below, units based on motion-energy filtering [12, 13, 14], units based on standard optical flow estimation techniques [6] and units based on algorithms for the estimation of principal texture direction [16] were utilized. All these disparity estimators can be realized by simple spatial filter operations combined with local nonlinearities; at least the units based on motion-energy filtering are currently discussed as models for cortical processing by complex cells.
The structure of the new network resembles superficially earlier cooperative schemes used to disambiguate false matches [8, 15], but the dynamics and the link structures of the new network are quite different. In the new scheme, the disparity stacks do not interact with each other; thus no direct spatial facilitation of disparity estimates is taking place. Such a spatial facilitation is a central ingredient of almost all other cooperative algorithms. Some small spatial facilitation enters coherence-based stereo only through the spatially extended receptive fields of the elementary disparity units used.
Interaction in the coherence detection occurs only along the lines defining the disparity stacks. Essentially, this interaction is of the excitatory type, while usual cooperative schemes have either none or inhibitory interactions along such lines. Furthermore, coherence detection is a fast and non-iterative process, whereas classical cooperative algorithms require many iterations before approaching some steady state.
Finally, the disparity units in classical cooperative schemes are basically binary units, indicating the existence or non-existence of a possible match. In coherence-based stereo, the disparity units are disparity estimators, giving back a guess of what value the correct disparity might have. For this reason, the disparity maps obtained by classical cooperative schemes and by the new coherence-based stereo algorithm have a very different quality: classical schemes return integer-valued maps, whereas the maps obtained with the new scheme have continuous values, displaying hyperacuity (i.e. sub-pixel precision).
Since coherence detection is an opportunistic scheme, extensions of the neuronal network to multiple spatial scales and to combinations of different types of disparity estimators is trivial. Additional units are simply included in the appropriate coherence stack. The coherence scheme will combine only the information from the coherently acting units and ignore the rest of the data. For example, adding units with asymmetric receptive fields [17] will result in more precise disparity estimates close to object boundaries.
Presumably, this is the situation in a biological context: various disparity units with rather random properties are grouped into stacks responding to common view directions. The coherence-detection scheme singles out precisely those units which have detected the true disparity. The responses of all other units are ignored.
| Prev: Coherence-based Stereo | Up: ^ Table of Contents ^ | Next: Numerical Results |
Comments are welcome! © 1997 by Rolf Henkel - all rights reserved.