Numerical Results
Figure 3 shows some results calculated with the new algorithm on two classical testimages. Data from several spatial scales was combined in each disparity stack to yield the final disparity maps. The results obtained with coherence-based stereo on these standard testimages are comparable to usual area-based approaches. The resulting disparity maps are dense with clearly defined object borders.
Figure 3: The performance of coherence-based stereo on classical testimages. A) The Pentagon. The overpasses are recovered well in the disparity map, and also some of the trees in the center of the building are visible. B) Renault automobile part. Even for the relative structureless background a good disparity estimate could be obtained. Both disparity maps were calculated with an input image size of 256x256 pixels.
Within the new coherence-based stereo algorithm, a simple verification
count can be derived from the relative number of coherently acting disparity
units in each stack, i.e. by calculating the ratio 
, where 
is the number of units in class 
. The verification count can be used to mark unreliable estimates.
Artificial stimuli, as well as images taken in technical context, are sometimes composed of large structureless regions. In those areas where the sensor noise is stronger than the intensity variation correlated with the object surfaces, a reliable estimation of disparities becomes impossible (parts of Figure 4E). With coherence-based stereo, these areas can be detected by a low verification count (Figure 4F). Using the verification count for masking all unreliable disparity estimates, coherence-based stereo can mimic a standard feature-based algorithm when confronted with difficult data (Figure 4G).
However, in contrast to classical feature-based approaches, none of the usual constraints basic to feature-based algorithms are explicitly build into the coherence detecting network. Also, with coherence-based stereo, disparity estimates will be obtained in all image areas with sufficient structure, regardless of the type of features present there. This is not the case with classical feature-based algorithms, where one gets estimates only in image regions with the preselected type of features.
Figure 4: When enough image detail is present, disparity is estimated by the new algorithm with subpixel precision (E). In other image areas, a low a verification count (F) indicates unreliable estimates. This can be used to mask unreliable data (G). A simple superposition of the left and right input pictures displays double contours (C), but the coherence detection scheme is able to fuse both stereo pictures to the cyclopean view of the scene (D). Note the change of perspective between the left and right input image and the cyclopean view.
As Figures 4E-G show in comparison to Figures 4A-B, the maps which are output by the coherence-based stereo algorithm are neither aligned with the left nor with the right view of the scene. This is a direct result of the network structure used (cmp. Figure 2). The diagonally running data lines in the network correspond to the lines of sight from the left and right eye positions, but the coherence detection is done within the vertical disparity stacks of the network. The links defining these stacks split the angle between the left and right data lines in half. Reprojecting data lines and coherence-detecting links back into 3D-space shows that the disparity stacks actually analyze the image data along view lines splitting the angle between left and right view directions in half, i.e., along the cyclopean view direction. Therefore, any data which is output by the coherence-based stereo algorithm is aligned with the cyclopean view of the scene.
It is very easy to obtain the cyclopean view of the scene itself. Let
and 
be the left and right input data of disparity unit 
, respectively. A simple summation over all coherently coding disparity
units,
gives the image intensities of the cyclopean view (Figure 4D).
Interestingly, the image constructed in this way is not severely distorted even in areas where the disparity estimate is poor. Note that the fusion of left and right input image to the cyclopean view is not an interpolation between the left and right image data. This can be seen by observing the change in perspective between the calculated cyclopean view and the left and right input images. The simple superposition of both stereo images (Figure 4C) displays in addition double contours which are absent in the cyclopean view.
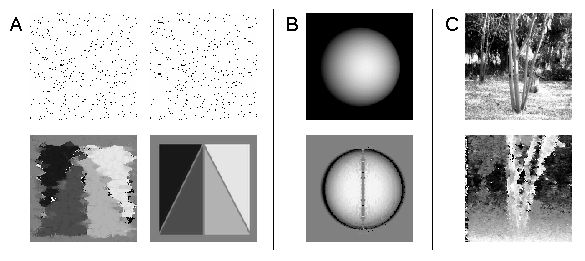
Figure 5: The new scheme works well with very different source images.
A) Filling-in occurs in sparse random-dot-stereograms from coarser spatial
channels (top: stereo pair with 3% black dots, bottom right: true disparity,
bottom left: calculated disparity). B) Images without any localized image-features
are also handled well. C) Dense disparity maps are obtained for image data
of natural scenery, which usually has sufficient detail for disparity estimation
in all image areas.
Coherence-based stereo works equally well with very different source images. In its multi-scale version, the coarser spatial channels interpolate disparity values at finer spatial channels when no estimate can be obtained there. Figure 5A displays results of a disparity calculation with a random-dot stereogram having only a pixel density of 3%. Due to filling-in, the true disparity map is recovered to a large extent even in image areas with no detail. In contrast to other cooperative schemes, the filling-in occurs in coherence-based stereo instantaneously; no iterative refinement or propagation of disparity values is necessary as with other approaches.
As already mentioned, various types of disparity estimators can be used within the basic algorithm. Fig. 5B shows results obtained with a disparity unit based on an algorithm for the estimation of principal texture direction. Classical feature-based stereo algorithms would fail with this stimulus set, since the stereo data lacks any localized images features [18]. Finally, in Fig. 5C, a disparity map obtained from an outdoor scene is shown. Natural imagery usually has sufficient detail present in all image areas and at all spatial scales, so dense and stable disparity maps can be obtained with the coherence-based stereo algorithm.
| Prev: Computational Structure | Up: ^ Table of Contents ^ | Next: Acknowledgements |
Comments are welcome! © 1997 by Rolf Henkel - all rights reserved.