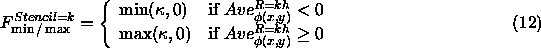
The above discussion explains why the min/max flow works; furthermore, it provides a nesting of flows designed to remove successively larger scales. By way of notation, we can now write that
Thus, a stencil of size k computes the average over a disk of
radius k h, where h is the discretization size. Roughly speaking,
we can see that this flow will attempt to remove structures of width
kh.
As an example, let 
, and return to the case of the disk.
Since the average will compute to a value close to the background color,
on this scale all structures are insignificant and the max flow
will be chosen everywhere, forcing the boundary to disappear.
We thus see that the min/max flow as defined in Eqn. 12 provides a hierarchy of scales that can be removed from a shape. In the next section, we apply this flow to a variety of images.
