 produces no
motion.
Consider now a flow of Stencil=1, in which we use the
average value of
produces no
motion.
Consider now a flow of Stencil=1, in which we use the
average value of 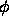 in a neighborhood of radius one unit h around the
point
in a neighborhood of radius one unit h around the
point 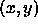 to tell us which flow to select;
to tell us which flow to select;



Consider the level set flow defined on a grid of size h, and
imagine that we have a shape with a perturbations on the boundary
of size one cell. As an example, we return to the black square on a white
background with notches given in Figure 4a.
We have just seen that the flow  produces no
motion.
Consider now a flow of Stencil=1, in which we use the
average value of
produces no
motion.
Consider now a flow of Stencil=1, in which we use the
average value of 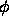 in a neighborhood of radius one unit h around the
point
in a neighborhood of radius one unit h around the
point 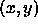 to tell us which flow to select;
to tell us which flow to select;
Here, 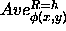 is defined as the average value of
is defined as the average value of
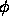 in a neighborhood of radius h around the point
in a neighborhood of radius h around the point 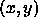 .
Similar to the above, each region attempts to ``convexify'' itself and hence
resists the other;
only in the notches is there some confusion as to which ``side''
the notch belongs.
In the notches, however, the sign of the average value of
.
Similar to the above, each region attempts to ``convexify'' itself and hence
resists the other;
only in the notches is there some confusion as to which ``side''
the notch belongs.
In the notches, however, the sign of the average value of 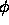 is the
opposite of the sign of the value at the notch. Hence, the notches do not
act as barriers, and the
``external'' flow (either black or white), is allowed to flow
through the notch, until the perturbation is removed.
Once the perturbation (i.e. notch) is removed, there are no remaining
first order structures; that is, nowhere are ``convex'' bumps (as seen
as either the black or white side) allowed to move.
Another way to characterize this is to say that the switch function
evaluates to zero when
it is impossible to further convexify one region without ``de-convexifying''
the other.
is the
opposite of the sign of the value at the notch. Hence, the notches do not
act as barriers, and the
``external'' flow (either black or white), is allowed to flow
through the notch, until the perturbation is removed.
Once the perturbation (i.e. notch) is removed, there are no remaining
first order structures; that is, nowhere are ``convex'' bumps (as seen
as either the black or white side) allowed to move.
Another way to characterize this is to say that the switch function
evaluates to zero when
it is impossible to further convexify one region without ``de-convexifying''
the other.
It is important to be clear about our definition of ``stopping''. The fact that curve stops is due to three effects. First, we embedding it in a level set framework. In fact our definition of the switch function assumes that a given curve is expressed as a level set of some higher dimensional function. Second, the calculation is performed on a grid. And third, the ``piling up'' of level sets, as discussed in the text, causes a shearing to develop in the level set function. The definition of ``stop'' here is that the curve motion has essentially gone to zero, and that running the calculation out for an extremely long time is required for any appreciable motion to occur.


