


Next: Min/Max Flow on
Up: The Switch Function
Previous: The Switch Function
Consider first the case of black disk on a white background, built in the
following way. We imagine initialization with the signed distance
function, with 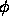 chosen as negative on the inside and
positive on the outside, and for display purposes, map all negative
chosen as negative on the inside and
positive on the outside, and for display purposes, map all negative
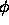 values into black and all positive
values into black and all positive  values into white.
Then the normal
values into white.
Then the normal 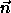 points from the black disk outwards towards
the white exterior.
As defined by
points from the black disk outwards towards
the white exterior.
As defined by 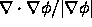 ,
the curvature of the boundary is positive.
Obviously then if we move this boundary under curvature flow,
i.e.,
,
the curvature of the boundary is positive.
Obviously then if we move this boundary under curvature flow,
i.e., 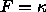 , the boundary will move inwards and the disk will disappear.
If we move the boundary under the flow
, the boundary will move inwards and the disk will disappear.
If we move the boundary under the flow 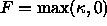 , the same
motion occurs, since the curvature of all the level curves is positive.
If we move this boundary under the flow
, the same
motion occurs, since the curvature of all the level curves is positive.
If we move this boundary under the flow 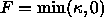 , the
shape will remain fixed.
, the
shape will remain fixed.
Let us define a flow, called 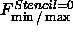 , as
follows:
, as
follows:
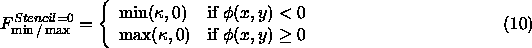
Our choice of the superscript ``Stencil=0'' means that we only use information
about the level set function 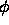 in a radius 0 around the point
in a radius 0 around the point
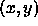 .
We now examine the effect of the above flow. All the level curves
in the black region corresponding to
.
We now examine the effect of the above flow. All the level curves
in the black region corresponding to 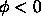 have positive curvature, hence they do not move, since the min function is
used and the speed function evaluates to zero at
such points. Conversely, all the level curves in the white region,
corresponding to
have positive curvature, hence they do not move, since the min function is
used and the speed function evaluates to zero at
such points. Conversely, all the level curves in the white region,
corresponding to 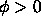 must move, since the curvature is positive
there and the speed function in the white region evaluates to the
curvature. Thus we see that in the above flow, the black region
acts a barrier to the attempts of the white exterior to move the
zero level set. Thus, the level curves ``pile up'' around the boundary
corresponding to the zero level set, but it does not move.
must move, since the curvature is positive
there and the speed function in the white region evaluates to the
curvature. Thus we see that in the above flow, the black region
acts a barrier to the attempts of the white exterior to move the
zero level set. Thus, the level curves ``pile up'' around the boundary
corresponding to the zero level set, but it does not move.
Conversely, suppose we exchange the roles of black and white, and
consider a white circle on a black background. We shall show that
the same thing occurs. This case corresponds to  in the interior
and
in the interior
and 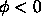 in the exterior. The normal points from out to the inside,
and the curvature (as defined by
in the exterior. The normal points from out to the inside,
and the curvature (as defined by 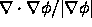 ) evaluates to negative.
Under our flow
) evaluates to negative.
Under our flow 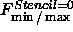 ,
we again examine the two regions. The level curves inside the white
region corresponding to
,
we again examine the two regions. The level curves inside the white
region corresponding to  all have negative curvature,
hence under
all have negative curvature,
hence under 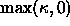 they cannot
move and act as a barrier; similarly, the level curves in black
region corresponding to
they cannot
move and act as a barrier; similarly, the level curves in black
region corresponding to 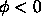 , all of whom have negative curvature,
attempt to move inwards, and are stopped by the frozen white mask.
Thus, the zero level set itself does not move.
, all of whom have negative curvature,
attempt to move inwards, and are stopped by the frozen white mask.
Thus, the zero level set itself does not move.
Thus, under the flow  , convex shapes
do not move. We now show that nonconvex shapes cannot move either.
Consider the four-pointed star-shaped region as given in
Figure 1(a), where the inside is black and
the outside is white. Inside the star-shaped region, the level
set function is negative, and hence the flow
, convex shapes
do not move. We now show that nonconvex shapes cannot move either.
Consider the four-pointed star-shaped region as given in
Figure 1(a), where the inside is black and
the outside is white. Inside the star-shaped region, the level
set function is negative, and hence the flow 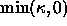 is
selected and attempts to move the concave regions, i.e. regions with negative
curvature. However, the level set function is positive outside
and suppresses the motion of concave regions due to the selection of
is
selected and attempts to move the concave regions, i.e. regions with negative
curvature. However, the level set function is positive outside
and suppresses the motion of concave regions due to the selection of
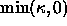 flow
(see Eqn. 10). The net effect is for the white region
to act as a barrier to the black region. Similarly, in convex regions
around the zero level set, the black region acts as a barrier to the motion
of the level sets in the white region. Thus, there is no motion of the
zero level set.
flow
(see Eqn. 10). The net effect is for the white region
to act as a barrier to the black region. Similarly, in convex regions
around the zero level set, the black region acts as a barrier to the motion
of the level sets in the white region. Thus, there is no motion of the
zero level set.
We summarize as follows; the flow given by 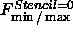 allows no motion of the boundary. This seems like a tremendous amount of
work to go through to achieve F=0 on the boundary, but we now show that a
speed function based on a larger stencil, i.e., one which includes more
points than just the value of
allows no motion of the boundary. This seems like a tremendous amount of
work to go through to achieve F=0 on the boundary, but we now show that a
speed function based on a larger stencil, i.e., one which includes more
points than just the value of 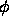 at
at  , produces motion.
, produces motion.



Next: Min/Max Flow on
Up: The Switch Function
Previous: The Switch Function
Bob Fisher
Fri Nov 7 13:12:05 GMT 1997
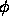 chosen as negative on the inside and
positive on the outside, and for display purposes, map all negative
chosen as negative on the inside and
positive on the outside, and for display purposes, map all negative
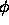 values into black and all positive
values into black and all positive  values into white.
Then the normal
values into white.
Then the normal 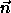 points from the black disk outwards towards
the white exterior.
As defined by
points from the black disk outwards towards
the white exterior.
As defined by 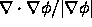 ,
the curvature of the boundary is positive.
Obviously then if we move this boundary under curvature flow,
i.e.,
,
the curvature of the boundary is positive.
Obviously then if we move this boundary under curvature flow,
i.e., 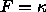 , the boundary will move inwards and the disk will disappear.
If we move the boundary under the flow
, the boundary will move inwards and the disk will disappear.
If we move the boundary under the flow 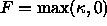 , the same
motion occurs, since the curvature of all the level curves is positive.
If we move this boundary under the flow
, the same
motion occurs, since the curvature of all the level curves is positive.
If we move this boundary under the flow 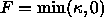 , the
shape will remain fixed.
, the
shape will remain fixed.



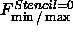 , as
follows:
, as
follows:
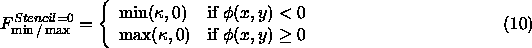
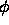 in a radius 0 around the point
in a radius 0 around the point
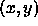 .
We now examine the effect of the above flow. All the level curves
in the black region corresponding to
.
We now examine the effect of the above flow. All the level curves
in the black region corresponding to 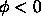 have positive curvature, hence they do not move, since the min function is
used and the speed function evaluates to zero at
such points. Conversely, all the level curves in the white region,
corresponding to
have positive curvature, hence they do not move, since the min function is
used and the speed function evaluates to zero at
such points. Conversely, all the level curves in the white region,
corresponding to 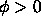 must move, since the curvature is positive
there and the speed function in the white region evaluates to the
curvature. Thus we see that in the above flow, the black region
acts a barrier to the attempts of the white exterior to move the
zero level set. Thus, the level curves ``pile up'' around the boundary
corresponding to the zero level set, but it does not move.
must move, since the curvature is positive
there and the speed function in the white region evaluates to the
curvature. Thus we see that in the above flow, the black region
acts a barrier to the attempts of the white exterior to move the
zero level set. Thus, the level curves ``pile up'' around the boundary
corresponding to the zero level set, but it does not move.
 in the interior
and
in the interior
and 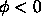 in the exterior. The normal points from out to the inside,
and the curvature (as defined by
in the exterior. The normal points from out to the inside,
and the curvature (as defined by 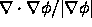 ) evaluates to negative.
Under our flow
) evaluates to negative.
Under our flow 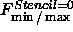 ,
we again examine the two regions. The level curves inside the white
region corresponding to
,
we again examine the two regions. The level curves inside the white
region corresponding to  all have negative curvature,
hence under
all have negative curvature,
hence under 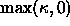 they cannot
move and act as a barrier; similarly, the level curves in black
region corresponding to
they cannot
move and act as a barrier; similarly, the level curves in black
region corresponding to 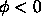 , all of whom have negative curvature,
attempt to move inwards, and are stopped by the frozen white mask.
Thus, the zero level set itself does not move.
, all of whom have negative curvature,
attempt to move inwards, and are stopped by the frozen white mask.
Thus, the zero level set itself does not move.
 , convex shapes
do not move. We now show that nonconvex shapes cannot move either.
Consider the four-pointed star-shaped region as given in
Figure
, convex shapes
do not move. We now show that nonconvex shapes cannot move either.
Consider the four-pointed star-shaped region as given in
Figure 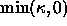 is
selected and attempts to move the concave regions, i.e. regions with negative
curvature. However, the level set function is positive outside
and suppresses the motion of concave regions due to the selection of
is
selected and attempts to move the concave regions, i.e. regions with negative
curvature. However, the level set function is positive outside
and suppresses the motion of concave regions due to the selection of
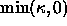 flow
(see Eqn.
flow
(see Eqn. 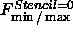 allows no motion of the boundary. This seems like a tremendous amount of
work to go through to achieve F=0 on the boundary, but we now show that a
speed function based on a larger stencil, i.e., one which includes more
points than just the value of
allows no motion of the boundary. This seems like a tremendous amount of
work to go through to achieve F=0 on the boundary, but we now show that a
speed function based on a larger stencil, i.e., one which includes more
points than just the value of 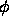 at
at  , produces motion.
, produces motion.