Although the Kalman filter was designed in the early 1960s to estimate the state of dynamic or time-varying systems, it can also be used on static systems as well. Altman [2] has used this technique to determine the structure of certain protein molecules using geometric information provided by nuclear magnetic resonance (NMR) studies. In this application, the inputs consist of geometric measurements such as distances and angles among various atoms (along with the variances of these measurements), and the output of the filter is a vector that lists all the coordinates of the atoms within the molecule.
Altman and Brinkley have also used a linear Kalman filter to extract
the boundaries of the kidney and the spleen from cross-sectional CT
images [3]. In this case, the output state vector (which
represents the boundary points of the organ) is updated by boundary
measurements that are introduced in a point-wise sequential fashion.
As more measurement points are introduced, the state vector estimate
converges to the true boundary. Hence, the Kalman filter provides a
Bayesian updating mechanism for sequentially refining the
estimate of the overall boundary vector. 
In other
words, it is a model-driven image segmentation technique. In both
cases, Altman is using the Kalman filter as a computational mechanism
for solving a geometric contraint-satisfaction problem. In the
protein structure problem, the constraints are the measured distances
and angles among atoms and the problem is to find the optimal
geometric configuration of these atoms that satisfies all the
constraints. In the organ segmentation problem, the constraints are
interactively supplied boundary points.
To illustrate how the Kalman filter can be used to solve a
geometric-constraint problem, I will discuss in greater detail the
kidney segmentation technique developed by Altman and Brinkley. In
this technique, the kidney cross-section is represented by a
two-dimensional radial contour model (RCM) in which the
organ boundary points are specified in polar coordinates relative to a
predefined kidney center [15] [16]. These
points are sampled at uniform angular intervals of 15 degrees
(although in theory, non-uniform angular intervals will work just as
well). An RCM with uniform angular displacements can be thought of as
a deformable bicycle wheel whose outer rim can be arbitrarily
stretched or compressed to match the boundary of the object it is
representing (see Figure 
). Here, the RCM is
initialized to look like an average kidney cross section (i.e., the
spokes are initialized to the mean boundary displacements computed
over a set of training images for each spoke). Starting from this
initial RCM (which also serves as a generic kidney model), the Kalman
filter incrementally refines all the displacements as boundary
points are introduced in a sequential fashion.
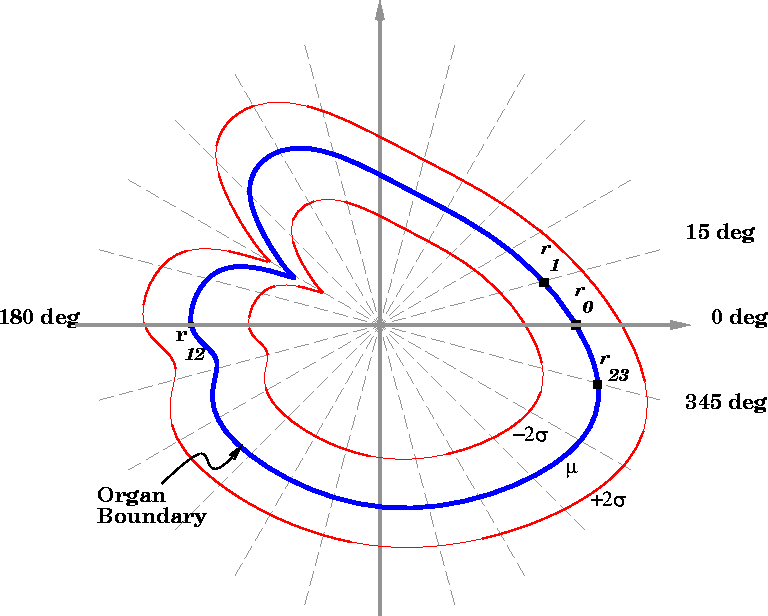
Figure: A representation of a kidney cross section using the Radial
Contour Model (RCM).
The state vector is made up of the 24 radial displacement values at each angular value ranging from 0 to 345 degrees:
The measurement vector is a subset of the state vector in
which only the displacements that are measured are present. For
example, if the measurement vector 
consists of two
components, the first at zero degrees and the second at 180 degrees,
the measurement model would look like the following:
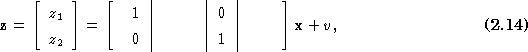
where the two non-zero columns represent the contributions
from 
and 
. Because the measurement vector is a
subsample of the state vector, the matrix H will consist entirely of
zeros and ones. The equation for generating a new estimate of the
state vector (denoted as 
), based on the previous state
estimate (denoted as 
) and a new measurement ,
was derived by Kalman as the following [46]:
Equation states that the magnitude of the update is a
weighted difference between the predicted measurement 
and the actual measurement . The weighting matrix
K is the Kalman filter that produces an optimal estimate of the new
state and is defined as follows:
The matrix 
is the state covariance matrix and is also updated
after each measurement according to the following equation:
This covariance matrix C captures the correlations among all the
state variables and permits the Kalman filter to make estimates about
the system's state using a relatively small set of measurements.
Indeed, before any measurements are made, the value of is
initialized to the covariance matrix computed on a set of training
data:
where the variance and covariance of the elements are defined in terms of the expected value of their cross-products:
and
The diagonal elements of C represent the variances of each
of the 24 radial displacements from the set of training
data. Equivalently, the value of 
is
initialized to the mean displacements computed from the training data:
The mean state vector 
can be thought of as the
a priori or generic model of the organ in the absence
of any measurements from an organ. Figure
illustrates how the mean and the variances of the generic model can be
used to define a region of high probability for finding the organ
boundary. This region is determined by bracketing the elements of the
mean state vector (labeled 
) by 
(note that
is unique for each of the 24 radial displacement elements).
As radial displacement measurements are made sequentially on an organ
to be segmented, the state vector and the 
brackets
converge toward the true boundary of the organ.
Altman and Brinkley verified the performance of their technique by demonstrating that it satisfied the following three properties:
brackets adequately describes the variations seen in actual test
cases. This was verified by comparing 15 test kidneys against the
generic model (which was generated using a different set of training
data). The authors found that all of the test cases had radial
displacements that were within two standard deviations from the
generic model. converges toward the actual organ boundary. This was
verified by computing an RMS error difference between the estimated
and the actual boundary. The authors noted that not only
was the error reduced for those radial elements that corresponded to
actual measurements, but the error was also reduced for radial
elements that were not measured. In other words, providing a single
new measurement reduces the error of each of the elements. This
effect is due to the information provided by the covariance matrix.
become smaller and smaller. Although this property may seem
intuitive, it is not readily apparent from equation .
The authors verified this property by inspecting the values along
the diagonal of C after each update.
As as result of their experiments with kidney cross sections, the authors concluded that the linear Kalman filter is capable of estimating the complete boundaries of kidneys from CT images using a limited set of boundary measurements. Furthermore, they demonstrated that the covariance matrix and the mean state vector can model both the geometry of the kidney and spleen cross sections as well as the variability seen in these organs. Hence, the Kalman filter technique can provide a statistical framework for modeling and extracting the boundaries of kidney sections. This statistical framework could behave more robustly certain in situations where deterministic algorithms fail.
