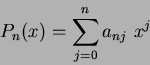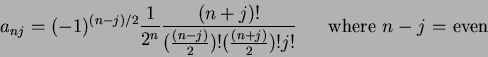

Next: Complex Zernike moments
Up: Orthogonal moments
Previous: Orthogonal moments
The Legendre moments [18] of order 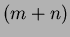 are defined as:
are defined as:
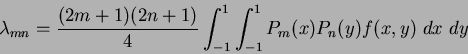 |
(45) |
where
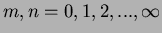 ,
, 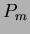 and
and 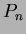 are the Legendre polynomials and
are the Legendre polynomials and 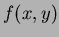 is the continuous image function.
The Legendre polynomials are a complete orthogonal basis set defined over the interval
is the continuous image function.
The Legendre polynomials are a complete orthogonal basis set defined over the interval ![$[-1,1]$](img163.png) .
For orthogonality to exist in the moments, the image function
.
For orthogonality to exist in the moments, the image function 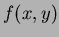 is defined over the same
interval as the basis set, where the
is defined over the same
interval as the basis set, where the 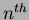 order Legendre polynomial is defined as:
order Legendre polynomial is defined as:
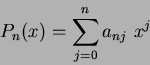 |
(46) |
and 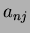 are the Legendre coefficients given by:
are the Legendre coefficients given by:
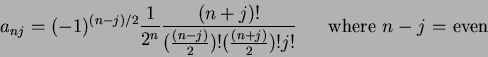 |
(47) |
So, for a discrete image with current pixel  , Equation 1.45 becomes:
, Equation 1.45 becomes:
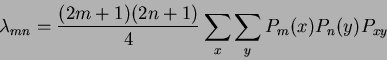 |
(48) |
and 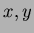 are defined over the interval
are defined over the interval ![$[-1,1]$](img163.png) .
.
Jamie Shutler
2002-08-15
![]() are defined as:
are defined as: