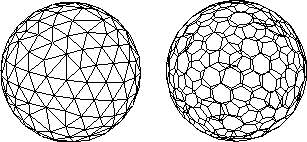
Figure 2: A triangluar mesh (left) and a dual simplex mesh (right)
Broadly speaking, a deformable meshing scheme (or model) consists of a template surface mesh and a mechanism to deform the template mesh. The surface mesh is a representation of a surface that consists of vertices, edges and faces. There are currently two distinct alternatives for the surface representation in the deformable meshing literature, namely triangular and simplex meshes. Exact definitions of these can be found from [2] and [1], respectively. Triangular meshes are composed of triangle faces which share each of their edges with exactly one other triangle face. Simplex meshes are topological duals of triangular meshes. A triangular mesh and a dual simplex mesh are shown in Fig. 2. The choice of the best representation depends on the application, but some insights are offered in [1].

Figure 2: A triangluar mesh (left) and a dual simplex mesh (right)
Regardless of the type of the mesh ![]() , it consists of
the set of discrete points, called mexels,
, it consists of
the set of discrete points, called mexels, ![]() and adjacency relations between mexels, which may be
modeled by a simple graph
and adjacency relations between mexels, which may be
modeled by a simple graph ![]() with vertices
with vertices ![]() . Then mexels
. Then mexels ![]() and
and
![]() are adjacent if and only if there is the edge ij in
are adjacent if and only if there is the edge ij in
![]() . Here we denote
mexels adjacent to mexel
. Here we denote
mexels adjacent to mexel ![]() by the symbols
by the symbols ![]() ,
, ![]() , where
, where ![]() is the number of adjacent mexels to the
mexel
is the number of adjacent mexels to the
mexel ![]() . With simplex meshes
. With simplex meshes ![]() is always 3.
is always 3.