

Next: Experiments
Up: Using SFS for Object
Previous: Direct Use of Needle-Map
The differential structure of a surface is captured by the local Hessian matrix, which may be approximated in terms of surface normals by
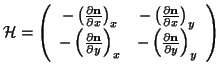 |
|
|
(3) |
where
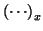 and
and
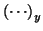 denote the x and y components of the parenthesized vector respectively.
denote the x and y components of the parenthesized vector respectively.
The principal curvatures of the surface are the eigenvalues of the Hessian matrix, found by solving
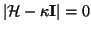 for
for 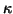 ,
where I is the identity matrix.
Koenderink and van Doorn[19] developed a single-value, angular measure to describe local surface topology in terms of the principal curvatures. This shape index is defined as
,
where I is the identity matrix.
Koenderink and van Doorn[19] developed a single-value, angular measure to describe local surface topology in terms of the principal curvatures. This shape index is defined as
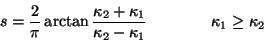 |
(4) |
and may be expressed in terms of surface normals thus
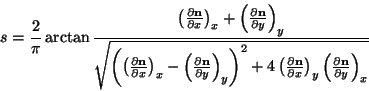 |
(5) |
Figure 1 shows the range of shape index values, the type of curvature which they represent, and the grey-levels used to display different shape-index values. Dark regions correspond to concavities, such as ruts, troughs and spherical caps, whilst light regions indicate caps, domes and ridges.
Figure:
The shape index scale ranges from -1 to 1 as shown. The shape index values are encoded as a continuous range of grey-level values between 1 and 255, with grey-level 0 being reserved for background and flat regions (for which the shape index is undefined).
 |


Next: Experiments
Up: Using SFS for Object
Previous: Direct Use of Needle-Map
Philip Worthington
1998-10-28
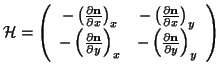
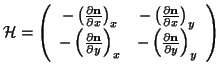
![]() for
for ![]() ,
where I is the identity matrix.
Koenderink and van Doorn[19] developed a single-value, angular measure to describe local surface topology in terms of the principal curvatures. This shape index is defined as
,
where I is the identity matrix.
Koenderink and van Doorn[19] developed a single-value, angular measure to describe local surface topology in terms of the principal curvatures. This shape index is defined as
