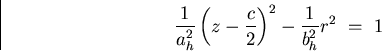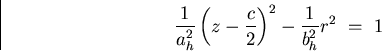Next: Resolution of a Catadioptric
Up: Specific Solutions of the
Previous: Ellipsoidal Mirrors
In Solution (16), when k>2 and c>0, we get the
hyperboloidal mirror:
| 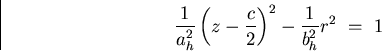 |
(27) |
where:
|  |
(28) |
As seen in Figure 7, the hyperboloid also yields a
realizable solution. The curvature of the mirror and the field of view
both increase with k. In the other direction (in the limit
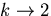 ) the hyperboloid flattens out to the planar mirror
of Section 2.3.1.
) the hyperboloid flattens out to the planar mirror
of Section 2.3.1.
Rees [Rees, 1970] appears to have been first
to use a hyperboloidal mirror with a perspective lens to achieve
a large field of view camera system with a single viewpoint.
Later, Yamazawa et al. [Yamazawa et al., 1993]
[Yamazawa et al., 1995] also
recognized that the hyperboloid is indeed a practical solution and
implemented a sensor designed for autonomous navigation.
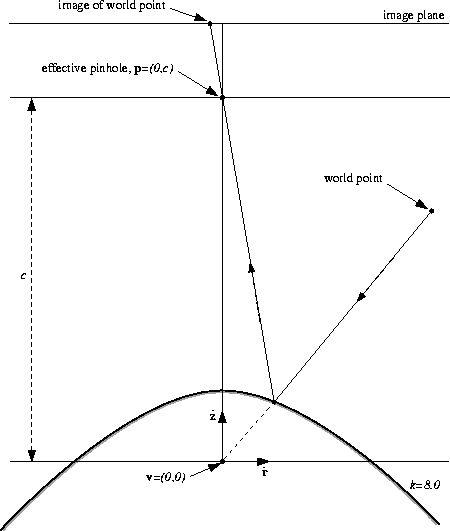
Figure 7:
The hyperboloidal mirror satisfies
the fixed viewpoint constraint when the pinhole and the viewpoint
are located at the two foci of the hyperboloid. This solution does
produce the desired increase in field of view. The curvature
of the mirror and hence the field of view increase with k.
In the limit 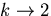 , the hyperboloid flattens to the
planar mirror of Section 2.3.1.
, the hyperboloid flattens to the
planar mirror of Section 2.3.1.
 |



Next: Resolution of a Catadioptric
Up: Specific Solutions of the
Previous: Ellipsoidal Mirrors
Simon Baker
1/22/1998