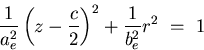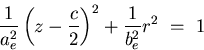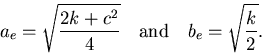Next: Hyperboloidal Mirrors
Up: Specific Solutions of the
Previous: Spherical Mirrors
In Solution (17), when k>0 and c>0, we get the
ellipsoidal mirror:
| 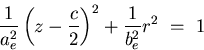 |
(25) |
where:
| 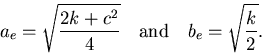 |
(26) |
The ellipsoid is the first solution that can actually be used to
enhance the field of view. As shown in Figure 6, if the
viewpoint and pinhole are at the foci of the ellipsoid and the
mirror is taken to be the section of the ellipsoid that lies below
the viewpoint (i.e. z < 0), the effective field of view is the
entire upper hemisphere 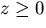 .
.
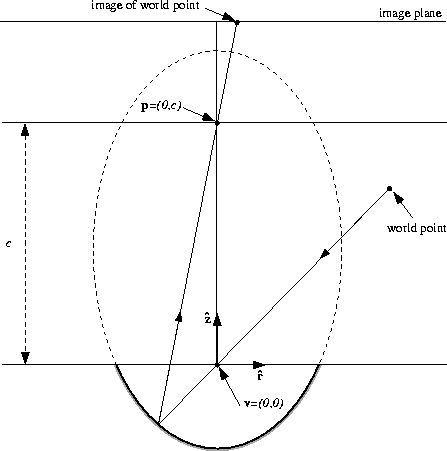
Figure 6:
The ellipsoidal mirror satisfies
the fixed viewpoint constraint when the pinhole and viewpoint are
located at the two foci of the ellipsoid. If the ellipsoid is
terminated by the horizontal plane passing through the viewpoint
z = 0, the field of view is the entire upper hemisphere
z > 0. It is also possible to cut the ellipsoid with other planes
passing through 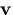 , but it appears there is to be little
to be gained by doing so.
, but it appears there is to be little
to be gained by doing so.
 |



Next: Hyperboloidal Mirrors
Up: Specific Solutions of the
Previous: Spherical Mirrors
Simon Baker
1/22/1998