


Next: Ellipsoidal Mirrors
Up: Specific Solutions of the
Previous: Conical Mirrors
In Solution (17), if we set c=0 and k>0, we get the
spherical mirror:
| 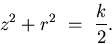 |
(23) |
Like the cone, this is a solution with little practical value. Since
the viewpoint and pinhole coincide at the center of the sphere, the
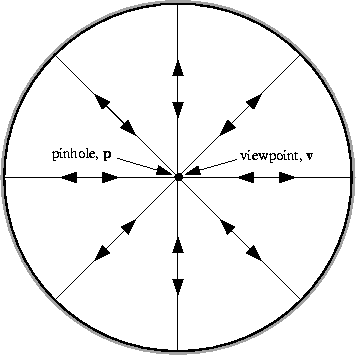
observer sees itself and nothing else, as is illustrated in
Figure 4.
Figure 4:
The spherical mirror satisfies the
fixed viewpoint constraint when the pinhole lies at the center of
the sphere. (Since c=0 the viewpoint also lies at the center of the
sphere.) Like the conical mirror, the sphere is of little
practical value because the observer can only see itself;
rays of light emitted from the center of the sphere are
reflected back at the surface of the sphere directly towards
the center of the sphere.
 |
The sphere has also been used to enhance the field of view several
times [Hong, 1991] [Bogner, 1995]
[Murphy, 1995]. In these implementations, the pinhole
is placed outside the sphere and so there is no single effective
viewpoint. The locus of the effective viewpoint can be computed in
a straightforward manner using a symbolic mathematics package.
Without loss of generality, suppose that the radius of the mirror is
1.0. The first step is to compute the direction of the ray of light
which would be reflected at the mirror point 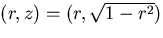 and then pass through the pinhole. This computation is
then repeated for the neighboring mirror point
and then pass through the pinhole. This computation is
then repeated for the neighboring mirror point 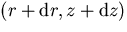 . Next, the intersection of these two rays is computed,
and finally the limit
. Next, the intersection of these two rays is computed,
and finally the limit  is taken while
constraining
is taken while
constraining 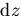 by
by 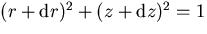 .The result of performing this derivation is that the locus of the
effective viewpoint is:
.The result of performing this derivation is that the locus of the
effective viewpoint is:
| ![\begin{displaymath}
\left(
\frac{c \left[ 1 + c (1 + 2 r^2) \sqrt{1-r^2} \right]...
...1-r^2}},
\frac{2 c^2 r^2}{1 + 2 c^2 - 3 c \sqrt{1-r^2}}
\right)\end{displaymath}](img72.gif) |
(24) |
as r varies from 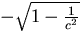 to
to
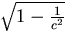 .The locus of the effective viewpoint is plotted for various
values of c in Figure 5.
.The locus of the effective viewpoint is plotted for various
values of c in Figure 5.
Figure 5:
The locus of the effective viewpoint of a circular mirror of radius
1.0 (which is also shown) plotted for c = 1.1 (a), c = 1.5 (b),
c = 3.0 (c),
and c = 100.0 (d). For all values of c, the locus lies within
the mirror and is of comparable size to the mirror.
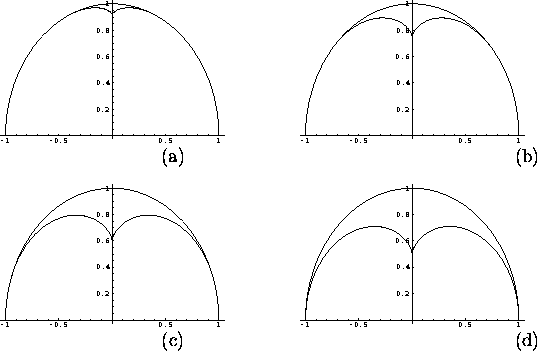 |
As can be seen, for all values of c the locus lies within
the mirror and is of comparable size to it.
Spheres have also been used in stereo applications
[Nayar, 1988] [Nene and Nayar, 1998], but as described
before, multiple viewpoints are a requirement for stereo.



Next: Ellipsoidal Mirrors
Up: Specific Solutions of the
Previous: Conical Mirrors
Simon Baker
1/22/1998

![]() and then pass through the pinhole. This computation is
then repeated for the neighboring mirror point
and then pass through the pinhole. This computation is
then repeated for the neighboring mirror point ![]() . Next, the intersection of these two rays is computed,
and finally the limit
. Next, the intersection of these two rays is computed,
and finally the limit ![]() is taken while
constraining
is taken while
constraining ![]() by
by ![]() .The result of performing this derivation is that the locus of the
effective viewpoint is:
.The result of performing this derivation is that the locus of the
effective viewpoint is:
![\begin{displaymath}
\left(
\frac{c \left[ 1 + c (1 + 2 r^2) \sqrt{1-r^2} \right]...
...1-r^2}},
\frac{2 c^2 r^2}{1 + 2 c^2 - 3 c \sqrt{1-r^2}}
\right)\end{displaymath}](img72.gif)