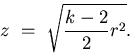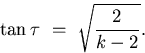Next: Spherical Mirrors
Up: Specific Solutions of the
Previous: Planar Mirrors
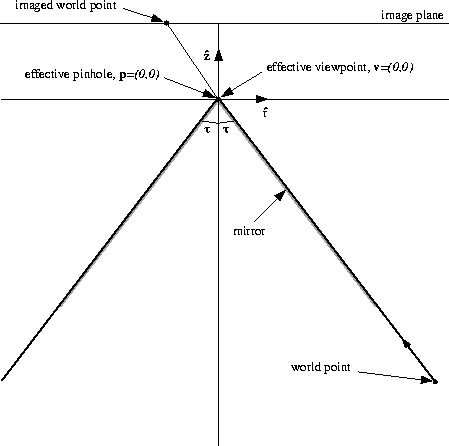
Figure 3:
The conical mirror is a solution of the
fixed viewpoint constraint equation. Since the pinhole is located at the
apex of the cone, this is a degenerate solution of little practical value.
If the pinhole is moved away from the apex of the cone (along the
axis of the cone), the viewpoint
is no longer a single point but rather lies on a circular locus.
If 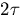 is the angle at the apex of the cone, the radius of the
circular locus of the viewpoint is
is the angle at the apex of the cone, the radius of the
circular locus of the viewpoint is 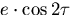 , where e is
the distance of the pinhole from the apex along the axis of the cone.
If
, where e is
the distance of the pinhole from the apex along the axis of the cone.
If 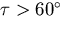 , the circular locus lies inside (below)
the cone, if
, the circular locus lies inside (below)
the cone, if 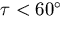 the circular locus lies outside (above)
the cone, and if
the circular locus lies outside (above)
the cone, and if 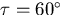 the circular locus lies on the
cone.
the circular locus lies on the
cone.
 |
In Solution (16), if we set c=0 and 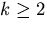 , we get
a conical mirror with circular cross section:
, we get
a conical mirror with circular cross section:
| 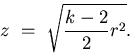 |
(20) |
See Figure 3 for an
illustration of this solution. The angle at the apex of the cone
is 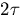 where:
where:
| 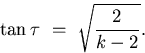 |
(21) |
This might seem like a reasonable solution, but since c=0 the pinhole
of the camera must be at the apex of the cone. This implies that
the only rays of light entering the pinhole from the mirror are the
ones which graze the cone and so do not originate from (finite extent)
objects in the world (see Figure 3.) Hence, the cone with
the pinhole at the vertex is a degenerate solution of no practical
value.
The cone has been used for wide-angle imaging a number of times
[Yagi and Kawato, 1990] [Yagi and Yachida, 1991] [Bogner, 1995].
In these implementations the pinhole is placed
quite some distance from the apex of the cone. It is easy to show that
in such cases the viewpoint is no longer a single point
[Nalwa, 1996]. If the pinhole lies on the axis of the cone at a
distance e from the apex of the cone, the locus of the effective
viewpoint is a circle. The radius of the circle is easily seen to be:
| 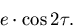 |
(22) |
If 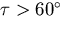 , the circular locus lies inside (below) the
cone, if
, the circular locus lies inside (below) the
cone, if 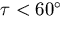 the circular locus lies outside (above)
the cone, and if
the circular locus lies outside (above)
the cone, and if 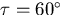 the circular locus lies on the cone.
the circular locus lies on the cone.



Next: Spherical Mirrors
Up: Specific Solutions of the
Previous: Planar Mirrors
Simon Baker
1/22/1998