Knowledge-based feature extraction in noisy data

Particularly difficult problems for data-driven recovery processes are outliers, low resolution and noisy data on reflective surfaces. When we have knowledge of either the specific parts or of general design relationships that hold in a particular domain, then we can exploit this knowledge in the shape recovery process.

Boundary relationships are standardized

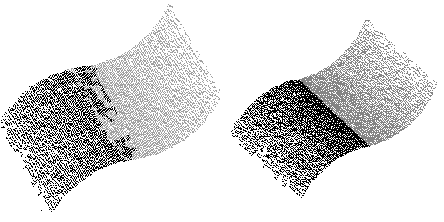
Figure 4 shows a surface fitting problem [41] where a cylindrical surface has a tangent join with another cylindrical surface. Data-driven surface fitting algorithms have trouble identifying a clean boundary, because surface shape variations are not distinguishable within the data noise. Using knowledge of the type of junction allows an accurate estimate of the interface and its parameters, such as the cylinder axes, radii and intersections in this example.

Figure 4: Cylinder/cylinder tangential surface interface with typical data-driven ragged fitting and a clean knowledge-based fitting.

Architectural model recovery can also exploit domain knowledge. Many recent part model and building representation systems are based on triangulation models [45], often recovered from raw range data. These models work well with smooth surfaces, but tend to round off surface crease edges or introduce artifacts on them. We have extended [32] the ``marching triangle'' surface triangulation and multiple surface fusion algorithm [24,25] to seed triangulation [11] at previously-located fold edges (using RANSAC [20]). This preserves the shape discontinuity at the fold edges while also allowing the accurate ``decimated'' triangulation of the marching triangle algorithm. Figure 5 shows part of an architectural scene without and with fold edge preservation.

Figure 5: Building fragment without and with fold edge preservation.

Alignment relationships are standardized

Figure 6 (left) shows noisy data for a row of holes [40]. The part being reconstructed is metallic so there is a lot of surface noise in the shape data arising from inter-reflections. In this case, as well as having a simple parametric model of the hole, we exploit additional user supplied knowledge about the part, namely that the holes are collinear, equally spaced and each row has equal radii holes. Using an optimization algorithm, we find the shape and position parameters that best describe the features, even with considerable noisy data.

Figure 6: Noisy data for a row of holes (left) and the fitted hole boundaries (right). A perpendicular view of the fitted holes, which are in light grey with the accepted edge points in darker grey.

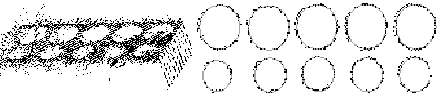Objects have standardized structures

We have recently applied this approach to architectural feature recovery, in this case using noisy and fragmentary 3D point cloud data [18]. While one could use constrained feature space search methods (e.g. [1,21]), here we use a constrained optimization method in which the constraints are built into the optimization process (e.g. [6]), to fit parametric shape models (e.g. [8,13,46]). While constraints are not well exploited in reverse-engineering [54], and often features are extracted independently (e.g. [4]), here we simultaneously fit, establish point-to-feature correspondences and estimate parameters. Using similar optimization methods as above, we extract the position and shape of a parametric model that best fits the data fragments, as well as effectively segmenting the data by assigning appropriate 3D points to the fitted model surfaces. Figure 7 shows an example doorway fit, where the doorway has 6 positional and 3 shape degrees of freedom.

Figure 7: a) Noisy incomplete data for a doorway, b) the fitted parametric model and selected data.