| |
(20) |
In many practical cases, the intrinsic parameters are unknown and the only information that can be be extracted from a sequence are point correspondences, which allow to compute a set of fundamental matrices. Autocalibration consist in computing the intrinsic parameters, or - in general - Euclidean information, starting from fundamental matrices (or, equivalently, from point correspondences). In this section we will see which constraints are available for the autocalibration.
In the uncalibrated case, the fundamental matrix can be computed form point correspondences. As we saw in Section 2.1, the seven parameters of the fundamental matrix are available to describe the geometric relationship between the two views (the epipolar geometry); the five parameters of the essential matrix are needed to describe the rigid displacement, thus at most two independent constraint are available for the computation of the intrinsic parameters from the fundamental matrix.
These two constraints must come from the characterization of essential
matrices given by Theorem 2.1. Indeed, the condition that
the matrix E has a zero singular value and two non-zero equal
singular values is equivalent to the following conditions, found by
Huang and Faugeras [25]:
This is an algebraic interpretation of the so-called rigidity
constraint, namely the fact that for any fundamental matrix ![]() there exist two intrinsic parameters matrix
there exist two intrinsic parameters matrix ![]() and
and
![]() and a rigid motion represented by
and a rigid motion represented by ![]() and
and ![]() such that
such that
![]()
By exploiting this constraint, Hartley [13] devised an algorithm to factorize the fundamental matrix that yields the five motion parameters and the two different focal lengths. He also pointed out that no more information could be extracted from the fundamental matrix without making additional assumptions (like, for example, that intrinsic parameters are constant).
A geometric interpretation of the rigidity constrain leads to the Kruppa equations, which will be briefly reviewed in Section 4.3.
The case of three views is not a straightforward generalization of the two-views case. The epipolar geometry can be described using the canonical decomposition introduced by Luong [30] or the trifocal tensor, both of which uses the minimal number of parameters, that turns out to be 18. The rigid displacement is described by 11 parameters: 6 for 2 rotations, 4 for two direction of translations and 1 ratio of translation norms2. Therefore, three views gives seven constraints on the intrinsic parameters. If they are constant, three views are sufficient to recover all the five intrinsic parameters.
In the general case of n views, Luong demonstrated that 11n - 15 parameters are need (at least) to describe the epipolar geometry, using his canonical decomposition. The rigid displacement is described by 6n -7 parameters: 3(n-1) for rotations, 2(n-1) for translations, and n-2 ratios of translation norms. There are, thus, 5n-8 constraints available for computing the intrinsic parameters.
As pointed out in [30], the n (n-1)/2 fundamental matrices are not independent, hence the n (n-1) constraints like (20) that can be derived from them are not independent. Nevertheless they can be used for computing the intrinsic parameters, since redundancy improves stability.
With a minimum of three displacements, we can obtain the internal parameters of the camera using a system of polynomial equations due to Kruppa [26], which are derived from a geometric interpretation of the rigidity constraint [31,8].
The unknown in the Kruppa equations is the matrix
![]() ,
called the Kruppa coefficients matrix, that
represents the dual of the image of the absolute conic (see
[6] for details). From
,
called the Kruppa coefficients matrix, that
represents the dual of the image of the absolute conic (see
[6] for details). From ![]() one can easily obtain the
intrinsic parameters by means of Cholesky factorization (
one can easily obtain the
intrinsic parameters by means of Cholesky factorization (![]() is
symmetric and positive definite ), or in closed form:
is
symmetric and positive definite ), or in closed form:
![\begin{displaymath}{\bf U} = \left [\begin{array}{c} {\bf u}_1^\top\\ {\bf u}_2^...
...top\end{array}\right ] \;\;\ {\bf
D} = \mathrm{diag}(r,s,0) .
\end{displaymath}](img80.gif)
In [28] the authors compare three solving methods: the homotopy continuation method, Levenberg-Marquardt and the Iterated Extended Kalman Filter. From the simulations reported, it appears that all the methods give comparable results. However, the homotopy continuation method is suitable for the case of few displacements, as it would be difficult to use all the constraints provided by a long sequence, and its computational cost would be too high. Iterative approaches (Levenberg-Marquardt and Iterated Extended Kalman Filter) are well suited to the case where more displacements are available. The main limitation of all these methods is the sensitivity to the noise in the localization of points.
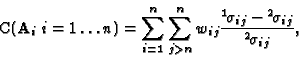 |
(23) |
The algorithm shows excellent convergence properties. Remarkably,convergence is achieved in the 90% of the cases, even when true values are perturbed with a relative error of 200% . On the other hand intrinsic parameters are recovered with fair, but not excellent, accuracy (5% with 5 views and 1.0 pixels standard deviation image noise).