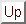

Next: Drainage Patterns
Up: CreasesSeparatrices and Drainage
Previous: Creases
Posterior attempts to characterize the drainage lines were based in the work of A. Cayley dated in 1859 [11]. Cayley considered local elevation maxima, minima and saddle points: summits, immits and knots, respectively, in his terminology. Cayley observed that in general the level curves around a knot consist of a family of concentric hyperbolas and stated that there are just two slopelines 'crossing' the knot: the ones intersecting each other at right angles (figure 6). He termed these slopelines ridge and course lines: for the ridge line the knot is a point of minimum elevation, for the course line it is a point of maximum elevation. The ridges are considered to end in a summit. Thus, a ridge line is a slopeline going from one summit to another through a single knot. Similarly, course lines are considered slopelines going from an immit to another through a single knot or, eventually, reaching the sea level instead of an immit.

Figure 6: Level curves and slopelines around a saddle (knot): there are two slopelines 'crossing' the knot. Notice that at the saddle point the gradient is not defined and so neither the slopelines. However here we can consider the saddle point as 'filling the gap', therefore, we say 'crossing' taking this fact into account.
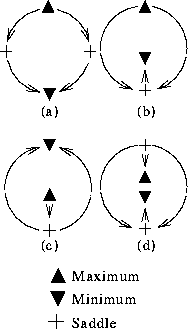
Figure 7: Canonical slope districts than can be constructed by following the slopelines 'crossing' saddle points until a maximum/minimum is reached.
In 1870 J. C. Maxwell [58] continued the work of Cayley. He also based his analysis in summits, immits and
knots. Maxwell stated that through each point of the earth's surface passes a slopeline which begins at a certain summit and ends in a certain immit. Then, he defined the basins as districts whose slopelines come from the same immit, and hills as districts whose slopelines run to the same summit. In this way the landscape may be naturally divided into basins and also, by an independent division, into hills, each point of the surface belonging to a certain basin and also to a certain hill. Watersheds were then defined as slopelines separating basins, and watercourses as slopelines separating hills.
Maxwell pointed out that the only method of determining a line of watershed/watercourse consists of firstly finding a saddle, secondly finding the two points of maximum/minimum height around the saddle (in figure 6: c,e maxima and b,d minima) and finally following the slopelines upwards/downwards until a summit/immit is reached. We have to interpret this affirmation not as a procedure but just as pointing out that watershed/watercourse analysis must be global. In fact, this procedure will give us separatrices that can be or not watersheds/watercourses: given a saddle point, the two
slopelines reaching a summit form a watershed together only if the two slopelines running down hill from the saddle
point drain to different immits (analogously for watercourses). If not, the slopelines are called virtual separatrices
[1]. Accordingly, we can describe a separatrix of the function 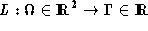 as follows. Let
as follows. Let 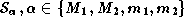 (figure 6) be a slopeline given in parametric form by the function
(figure 6) be a slopeline given in parametric form by the function 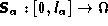 , defined as
, defined as
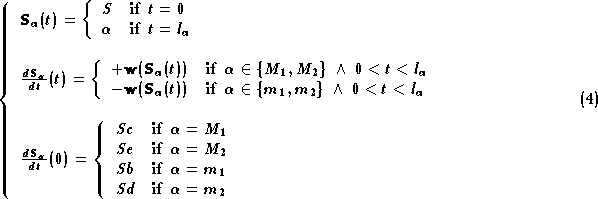
where 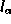 is the length of
is the length of 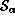 , the
, the 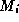 are maxima of L, the
are maxima of L, the 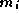 are minima and S is the saddle point which is 'crossed' by the
two special slopelines that meet each other at right angles and
are minima and S is the saddle point which is 'crossed' by the
two special slopelines that meet each other at right angles and 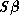 , with
, with 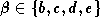 , is the vector from S to
, is the vector from S to 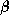 (figure 6). Then the curve
(figure 6). Then the curve

is a ridge-like separatrix and the curve

is a valley-like separatrix. In figure 6, the ridge-like separatrix of equation (5) is a line of watershed if the minima from which the saddle S is reached are different, this is, 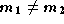 . Analogously, the valley-like separatrix is a watercourse if
. Analogously, the valley-like separatrix is a watercourse if 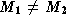 . Watersheds/watercourses and virtual separatrices together form the separatrices of the landscape. Furthermore, as critical points and slopelines (on the landscape plane) are conserved by monotonic height transforms, separatrices
are invariant to them. Moreover, they are also invariant under rotations and translations of the spatial axes, as well as uniform scaling of them.
. Watersheds/watercourses and virtual separatrices together form the separatrices of the landscape. Furthermore, as critical points and slopelines (on the landscape plane) are conserved by monotonic height transforms, separatrices
are invariant to them. Moreover, they are also invariant under rotations and translations of the spatial axes, as well as uniform scaling of them.
With respect to the drainage patterns,
it is clear that watercourses do not sketch the drainage pattern, since
there are channels that can just start in the top of the mountain and go downhill to an
immit or to the see level without pass through any saddle (e.g. the channel along a
ravine). Jordan took this fact into account in a series of discussions with Mr. Boussinesq [41, 42, 40] and states that in the bottom of a valley the only way of knowing what is the special slopeline where the other converge, is looking at their origin: the special slopeline is the one starting at a saddle point or at a double inflection point of the level curves (that is what takes into account channels along ravines). Other example 'against' separatrices is given in [75] and, more recently, in [45]: a separatrix is marked as channel collector in a landscape where water drains to a minimum through an extended surface instead of by a special stream. This example, however, is revised by Rieger in [72] who affirms that it reproduces a non-generic situation.
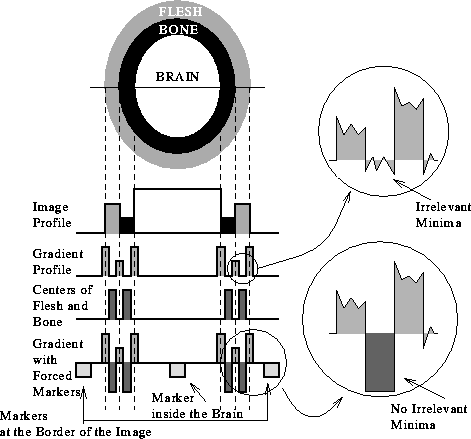
Figure 8: Scheme of the profile of a MR slice. To segment brain, bone and flesh we can compute the watersheds of the gradient image, imposing as markers (forced minima) the middle (valley-like SA) of the bone, the middle (ridge-like SA) of the flesh, a point inside the brain and the border of the image.
Recently, Nackman [66] formulated the work of Maxwell in terms of the so-called slope districts. A slope district is defined as the overlapping region between a basin and a hill. Nackman concluded that there are just four types of slope districts in a 2-dimensional Morse function (figure 7). Morse functions are those having a finite number of critical points which, besides, are isolated and non-degenerated. Conceptually, the slope districts are a generalization to smooth functions of two variables of the intervals of constant first derivative sign in the one variable case: all the slopelines of a given district reach a single maximum from a single minimum.
Griffin [29, 30] extracted the ridge and course lines proposed by Cayley, Maxwell, Jordan and
Nackman from a digital image. He first detects the singular points and then connects them by slopelines
through saddle points. Rosin stated [73, 74] that the fourth type of slope district defined by Nackman is unstable ((d) in figure 7), and through
experiments based in a number of different kind of digital 2-dimensional images, he concluded that the more frequent type is the first one. This basically means that almost all the separatrices are watersheds or watercourses. Rosin defined a watershed line as a ridge line that separates the flow of draining water from a
single peak towards two valley bottoms. Analogously, he defined a watercourse line as a trough line that separates the flow of water into a
single valley bottom which comes from two peaks. Then the slope districts are extracted in a region--reasoning fashion instead of tracking the watercourses and watersheds of the image: the image is partitioned into hills and basins and afterwards the slope
districts are identified as the intersection of both types of region.
Parallelly the mathematical morphology school has presented several algorithmic definitions of watersheds [15] in digital spaces. The most efficient algorithm, due to Luc Vincent [93], is based on an immersion process analogy, in which the flooding of water in the image is efficiently simulated by using hierarchical queues. Najman [67] extended the algorithmic watershed definition to continuous Morse functions concluding that, actually, the algorithmic definition for discrete spaces
'converge' to the continuous case, this is, watersheds/watercourses follow the gradient direction of the function while acting as separatrices.

Figure 9: From top to bottom and left to right: (a) MR slice. (b) The same slice smoothed by a Gaussian. (c) Gradient of the smoothed slice. (d) Watershed of the gradient, showing the oversegmentation problem. (e) Watersheds of the smoothed image in (b). (f) Watercourses of the smoothed image in (b). (g) Creases (ridge and valley like) by thresholding the value of  , according with the implementation given in [52], and thinning the result of the threshold. (h) Crease points from previous image grouped in crease segments and colored according with its length: the longest the lightest. (i) Markers for the watershed algorithm: the two longest creases from (h), an interior point of the brain and the border of the image. (j) Regions found by the watershed algorithm applied to edgeness image using markers (forced minima) from (i). (k) Watersheds (boundaries of the previous regions) over the original image. (l). Creases obtained thresholding
, according with the implementation given in [52], and thinning the result of the threshold. (h) Crease points from previous image grouped in crease segments and colored according with its length: the longest the lightest. (i) Markers for the watershed algorithm: the two longest creases from (h), an interior point of the brain and the border of the image. (j) Regions found by the watershed algorithm applied to edgeness image using markers (forced minima) from (i). (k) Watersheds (boundaries of the previous regions) over the original image. (l). Creases obtained thresholding  applied to the gradient image.
applied to the gradient image.
In artificial vision, however, due to the fact that separatrices divide the image in closed regions, they are typically involved in the computation of the folds of  . Crowley and Parker also extracted the separatrices of their multiresolution transform. As we can see through the example in figure 9,
though, the partition of
the image into basins, dales or together (slope districts) turn out in an oversegmentation. In figure 9((d) we extracted watersheds/watercourse with the algorithm given in [93, 15], but the oversegmentation is also present by using algorithms which extract separatrices as the given in [29, 30, 73, 28, 74], since the oversegmentation problem is due to the presence of a number of irrelevant critical points. Therefore, the extraction of separatrices is combined with methods for grouping similar
(according with a presetted criterion) slope districts or are analyzed in a
space-scale setting, as can be seen through the given references. Other approach to deal with oversegmentation is the given by the watershed
algorithm. It allows to define the set of minima (maxima for watercourses) to
be considered instead of the minima of the analyzed image, which reduce oversegmentation and drive the algorithm to interesting structures.
As example, let's examine the problem of figure 9:
. Crowley and Parker also extracted the separatrices of their multiresolution transform. As we can see through the example in figure 9,
though, the partition of
the image into basins, dales or together (slope districts) turn out in an oversegmentation. In figure 9((d) we extracted watersheds/watercourse with the algorithm given in [93, 15], but the oversegmentation is also present by using algorithms which extract separatrices as the given in [29, 30, 73, 28, 74], since the oversegmentation problem is due to the presence of a number of irrelevant critical points. Therefore, the extraction of separatrices is combined with methods for grouping similar
(according with a presetted criterion) slope districts or are analyzed in a
space-scale setting, as can be seen through the given references. Other approach to deal with oversegmentation is the given by the watershed
algorithm. It allows to define the set of minima (maxima for watercourses) to
be considered instead of the minima of the analyzed image, which reduce oversegmentation and drive the algorithm to interesting structures.
As example, let's examine the problem of figure 9:
we want to segment a MR slice (figure 9(a)) into its three main components which are, from the head outside to its inside: flesh (exterior white ring), bone from the skull (interior black ring) and brain (the rest but without following the sulci contours, in this case). We want to perform the segmentation by extracting the ridge-like structures from the gradient (figure 9(c)) of a smoothed version of the MR slice (figure 9(b)). Smoothing was done in the scale-space setting, by convolving with a Gaussian of standard deviation  [36, 85, 86]. The watersheds of the gradient (figure 9(d)) produce a oversegmentation due to irrelevant minima.
Therefore, we need markers: we will substitute the minima of the gradient image by another set of minima, in such a way that the separation of the basins induced by these minima would produce the pursued segmentation. A suitable set of minima
consist of the center of the flesh ring (ridge-like SA), the center of the bone (valley-like SA), any point inside the brain and the border of the image (figure 8). At first glance we can think on applying the watershed
algorithm to the smoothed MR slice to obtain the ridge-like flesh SA, and
the same to the inverse of the smoothed MR slice to obtain the valley-like
bone SA. The results can be seen in figures 9(e) and 9(f), respectively. Although we can distinguish clearly the ridge-like structure constituting the SA of the flesh, to actually isolate it we should run an intelligent grouping process or do it manually.
The same (oversegmentation) problem is present to extract the valley-like structure of the bone's SA. Because the oversegmentation, we decide to use crease detection based on
[36, 85, 86]. The watersheds of the gradient (figure 9(d)) produce a oversegmentation due to irrelevant minima.
Therefore, we need markers: we will substitute the minima of the gradient image by another set of minima, in such a way that the separation of the basins induced by these minima would produce the pursued segmentation. A suitable set of minima
consist of the center of the flesh ring (ridge-like SA), the center of the bone (valley-like SA), any point inside the brain and the border of the image (figure 8). At first glance we can think on applying the watershed
algorithm to the smoothed MR slice to obtain the ridge-like flesh SA, and
the same to the inverse of the smoothed MR slice to obtain the valley-like
bone SA. The results can be seen in figures 9(e) and 9(f), respectively. Although we can distinguish clearly the ridge-like structure constituting the SA of the flesh, to actually isolate it we should run an intelligent grouping process or do it manually.
The same (oversegmentation) problem is present to extract the valley-like structure of the bone's SA. Because the oversegmentation, we decide to use crease detection based on  according with the implementation given in [52]. In figure 9(g) we see the obtained creases (both ridge and valley like). In figure 9(h) the crease points from previous image are grouped in crease segments and colored according with its length: the longest the lightest. We used 8-connectivity to link crease points.
In figure 9(i) we show the markers that we will use in the watershed algorithm: the two creases from 9(h), an interior point of the brain (e.g. center of masses of the interior crease from the two selected) and the border of the image.
In figure 9(j) we can see the regions found by the watershed algorithm applied to the edgeness image using as markers (forced minima) the white pixels shown in 9(i). In figure 9(k) are shown the watersheds (boundaries of the previous regions) over the original image (lowering its dynamic range for visualization purposes). Finally, figure 9(l) show the creases obtained by applying the
according with the implementation given in [52]. In figure 9(g) we see the obtained creases (both ridge and valley like). In figure 9(h) the crease points from previous image are grouped in crease segments and colored according with its length: the longest the lightest. We used 8-connectivity to link crease points.
In figure 9(i) we show the markers that we will use in the watershed algorithm: the two creases from 9(h), an interior point of the brain (e.g. center of masses of the interior crease from the two selected) and the border of the image.
In figure 9(j) we can see the regions found by the watershed algorithm applied to the edgeness image using as markers (forced minima) the white pixels shown in 9(i). In figure 9(k) are shown the watersheds (boundaries of the previous regions) over the original image (lowering its dynamic range for visualization purposes). Finally, figure 9(l) show the creases obtained by applying the  based
crease detector to the gradient image. The result is not bad, but it is clear the necessity of a post-processing step in order to obtain the desired closed boundaries, this is, as in figure 9(k).
based
crease detector to the gradient image. The result is not bad, but it is clear the necessity of a post-processing step in order to obtain the desired closed boundaries, this is, as in figure 9(k).
This example shows
that the watershed algorithm combined with an appropriate set of markers is
a powerful tool. On the other hand, there are cases where separatrices schemes are not useful due to the fact of its global character:
it could happen that a whole curve can not be extracted because an 'opportune'
critical point is not present. For example, in the medialness measure of figure
5(b) there are not local minima and, therefore, the watershed
algorithm, for example, can not extract the ridge-like structure. Moreover, there is not a clear way of putting markers to make the watershed algorithm to
work. In general, this global character is mainly affected when changing the Field of View of the scene, since extrema on its border are thrown away (in medical imaging this can be a big problem is some cases).


Next: Drainage Patterns
Up: CreasesSeparatrices and Drainage
Previous: Creases
Antonio Lopez
Wed Oct 8 17:04:50 MET DST 1997