According to Professors J. J. Koenderink and A. J. van Doorn[45] and text books on descriptive geometry [64] the proper mathematical characterization of the special slopelines that form the drainage pattern of a terrain, goes back to 1915 and is due to R. Rothe who identifies them as (parts of) slopelines where other slopelines converge and eventually join them (sometimes at the infinity) to form a channel stream [75]. Mathematically, these special slopelines are singular solutions of the Ordinary Differential Equation (ODE) defining the slopeline family. For
![]()
being the ODE, or 1-form, defining the slopeline family, where ![]() , it is well-known that it is not an exact form since it is not closed (
, it is well-known that it is not an exact form since it is not closed ( ![]() exact
exact ![]()
![]() closed). We omit here these details since it would mean go to exterior calculus. The idea is that, due to the fact that
closed). We omit here these details since it would mean go to exterior calculus. The idea is that, due to the fact that ![]() is not exact, we can express it as
is not exact, we can express it as
![]()
where ![]() and
and ![]() are not uniquely defined functions. After a rather non-trivial geometric reasoning [75, 45] Rothe concluded that the special slopelines drawing the drainage pattern are characterized by the condition
are not uniquely defined functions. After a rather non-trivial geometric reasoning [75, 45] Rothe concluded that the special slopelines drawing the drainage pattern are characterized by the condition
![]()
Since the equation of the slopelines remains invariant under arbitrary monotonic transformations of the height axis, Rothe's drainage lines are also invariant under such transforms. They are also invariant under rotations and translations of the spatial axes.
However, the discussion about what is the right characterization of these special slopelines still remains. In [72] Rieger supported Jordan's definition (slopelines through saddle points or through points of double inflection of the level curves) as more 'plausible' than Rothe's one.
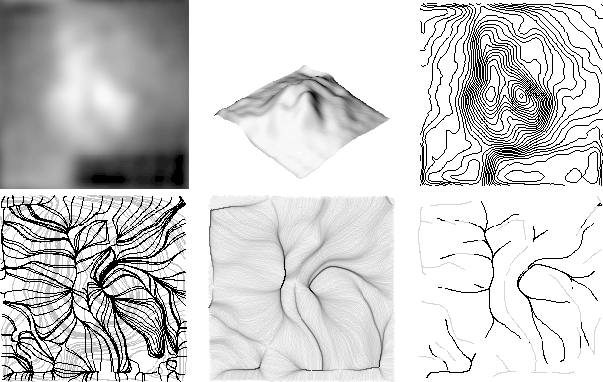
Figure 10: From top to bottom and left to right: (a) Heart gammagraphic image. (b) Image seen as a landscape. (c) Level curves. (d) Some slopelines
(black) over the level curves (grey). Observe how slopelines crowd along special slopeline segments. (e) Accumulation image where
darker grey-levels denote greater accumulation. (f) Selected special slopelines segments: drainage pattern (grey) and inverse drainage pattern (dark).
From the viewpoint of artificial vision this discussion is not so much important. We
will use the definition that best works at any given problem. Following this principle,
in [53] we presented an implementation of Rothe's definition , this is, based on curve reasoning over the convergence of the slopelines of the landscape, but without checking whether slopelines pass though a minimum (figure 10). We used the accumulation of water runoff along slopelines to drive the search to the special ones. Afterwards we pruned the resulting slopelines according to criteria as curve length and overlapping
among curves. In fact, since results on several types of images were encouraging, we look further to do some work to improve the algorithm.
, this is, based on curve reasoning over the convergence of the slopelines of the landscape, but without checking whether slopelines pass though a minimum (figure 10). We used the accumulation of water runoff along slopelines to drive the search to the special ones. Afterwards we pruned the resulting slopelines according to criteria as curve length and overlapping
among curves. In fact, since results on several types of images were encouraging, we look further to do some work to improve the algorithm.
Without our knowledge, previous works were done that can be considered to follow Rothe's idea, at least in my opinion as I would justify in short. This is due to the fact that the process of generating the drainage networks can be thought in a natural way, for example, the following was the manual approach of Speight [82] in 1968: he drew a square grid of points spaced 30.5 meters, on a contour map; then a slopeline perpendicular to the level curves was traced downhill from each grid point; and, finally, a line segment of length 30.5 meters was centered, on each grid point, parallel to the level curves, and if the number of slopelines crossing it was greater than 100 or if the line had a density over a `narrow zone of flow concentration' of more than 1/0.305 slopelines/meter the point was declared to lie on a `watercourse'. This kind of algorithm is known as runoff simulation. Therefore, this kind of simulation basically measures the amount of water coming to a discrete cell. This amount can be associated to the slopelines passing trough the cell, in such a way that the special (part of) slopeline representing a channel is expected to have a high amount of water along all the discrete cells that it passes. Notice that the relative amount of water on the cells of a region is quite stable when we reduce the region of interest (ROI). What changes is the absolute amount of water, since there would be less points from which water runoff comes. Furthermore, removing of critical points relatively far away from the ROI do not affect the runoff of that region, and so the location of the special slopelines representing the channels of the region. Algorithms extracting separatrices are affected by this phenomena (figure 11). On the other hand, if you translate convergence of slopelines in the continuous case, from Rothe's definition, as overlapping of discrete slopelines for digital images, we can assume that slopelines join before arriving to a minimum (as Rothe predicts) along a whole segment that will finish at the minimum. Moreover, to avoid the problem of the ROI, we can assume that the minimum is placed out of this ROI. Notice that this fact will not affect the relative accumulation of water in the ROI. Therefore, in my opinion, if in a given region of interest we look for special discrete slopelines where the others overlap, therefore, along which water is accumulated, we follow basically Rothe's definition since we do not need to look for critical points to single out the discrete slopelines connecting them.

Figure 11: From left to right: (a) Level curves of a heart gammagraphic image. (b) Watercourses on the original gammagraphic image. The algorithm described in [93] was applied. An important channel at the center of the image, on the heart, is missing since an 'opportune' maxima is not present. (c) drainage pattern by following Rothe's definition. The channel on the heart is detected (pointed by the black arrow).
People working with real earth data, such as Digital Elevation Models (DEM), extract drainage patterns by more or less sophisticated runoff simulations (we omit here a systematic list of details), since they are also interested in a real amount of water that eventually could receive certain earth region. In [53] we use a simple accumulation process since we were not interested in the precise amount of water (of any digital image) but just in the drainage network as a hierarchy of curves. Mark [57] proposed the extraction of the drainage network from DEMs by simulating runoff concentration, with those cells receiving simulated surface runoff above some predetermined threshold being declared to be on the drainage network. The runoff scheme was extended in [68] by O'Callaghan and Mark, through a sequence of procedures, starting with the smoothing of the original DEM, an accumulation process by following gradient directions, deciding whether a point is on a drainage line according with a threshold value on its accumulation (flow received), and a final process of linking drainage points to form a net of drainage lines. Seemuller [78] went deeply on the extraction of the drainage pattern in vector form from the raster accumulation given by the runoff simulation. He obtained a branching hierarchy of the network in nested list data format. In this way the information is more compact (drainage matrices are sparse) and it is possible to classify drainage networks into several standard forms (e.g. dendritic, trellis, etc) which constitutes a clue to the type of soil or rock comprising the terrain [94, 84].
More efficient algorithms for runoff extraction have been recently presented [81]. They rely on first eliminating irrelevant minima to ensure the continuity of streamlines [80]. These minima are considered to be spurious errors at the spatial resolution of an usual DEM. After this step the runoff is simulated by assigning to each pixel the gradient direction as flow direction and computing the quantity of water (accumulation) that each pixel receives by means of techniques based on hierarchical queues. Drainage networks are then extracted by thresholding the accumulation. McCormack [59] also presented an efficient algorithm extracting drainage networks and watersheds at the same time.
It has not been proved (at least as far as I know) that the runoff simulation followed by a thresholding
on the accumulation gives drainage patterns whose lines are discrete slopelines. However, due to the construction
of the algorithm, it is quite plausible. For example, the watershed algorithm has been proved to give lines
that tend to be discrete slopelines [67].
At this point, we conclude by summarizing in table 1 some of the main features of the different ridge/valley-like structures we have reviewed.
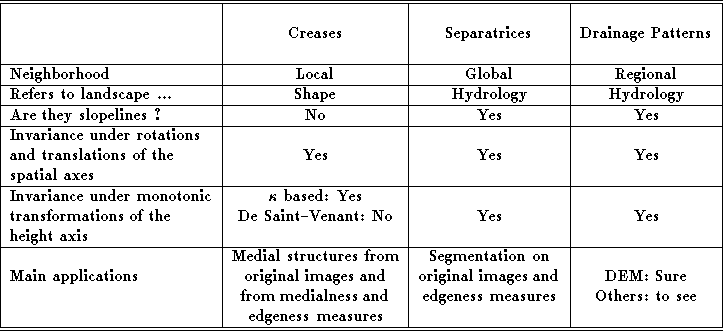
Table 1: Summary of properties of ridge/valley-like structures.