





Edges are places in the image with strong intensity contrast. Since edges often occur at image locations representing object boundaries, edge detection is extensively used in image segmentation when we want to divide the image into areas corresponding to different objects. Representing an image by its edges has the further advantage that the amount of data is reduced significantly while retaining most of the image information.
Since edges consist of mainly high frequencies, we can, in theory, detect edges by applying a highpass frequency filter in the Fourier domain or by convolving the image with an appropriate kernel in the spatial domain. In practice, edge detection is performed in the spatial domain, because it is computationally less expensive and often yields better results.
Since edges correspond to strong illumination gradients, we can highlight them by calculating the derivatives of the image. This is illustrated for the one-dimensional case in Figure 1.
Figure 1 1st and 2nd derivative of an edge illustrated in one dimension.
We can see that the position of the edge can be estimated with the maximum of the 1st derivative or with the zero-crossing of the 2nd derivative. Therefore we want to find a technique to calculate the derivative of a two-dimensional image. For a discrete one-dimensional function f(i), the first derivative can be approximated by
Calculating this formula is equivalent to convolving the function with [-1 1]. Similarly the 2nd derivative can be estimated by convolving f(i) with [1 -2 1].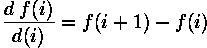
Different edge detection kernels which are based on the above formula enable us to calculate either the 1st or the 2nd derivative of a two-dimensional image. There are two common approaches to estimate the 1st derivative in a two-dimensional image, Prewitt compass edge detection and gradient edge detection.
Prewitt compass edge detection involves convolving the image with a set of (usually 8) kernels, each of which is sensitive to a different edge orientation. The kernel producing the maximum response at a pixel location determines the edge magnitude and orientation. Different sets of kernels might be used: examples include Prewitt, Sobel, Kirsch and Robinson kernels.
Gradient edge detection is the second and more widely used technique. Here, the image is convolved with only two kernels, one estimating the gradient in the x-direction, Gx, the other the gradient in the y-direction, Gy. The absolute gradient magnitude is then given by
and is often approximated with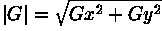
In many implementations, the gradient magnitude is the only output of a gradient edge detector, however the edge orientation might be calculated with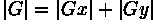
The most common kernels used for the gradient edge detector are the Sobel, Roberts Cross and Prewitt operators.
After having calculated the magnitude of the 1st derivative, we now have to identify those pixels corresponding to an edge. The easiest way is to threshold the gradient image, assuming that all pixels having a local gradient above the threshold must represent an edge. An alternative technique is to look for local maxima in the gradient image, thus producing one pixel wide edges. A more sophisticated technique is used by the Canny edge detector. It first applies a gradient edge detector to the image and then finds the edge pixels using non-maximal suppression and hysteresis tracking.
An operator based on the 2nd derivative of an image is the Marr edge detector, also known as zero crossing detector. Here, the 2nd derivative is calculated using a Laplacian of Gaussian (LoG) filter. The Laplacian has the advantage that it is an isotropic measure of the 2nd derivative of an image, i.e. the edge magnitude is obtained independently from the edge orientation by convolving the image with only one kernel. The edge positions are then given by the zero-crossings in the LoG image. The scale of the edges which are to be detected can be controlled by changing the variance of the Gaussian.
A general problem for edge detection is its sensitivity to noise, the reason being that calculating the derivative in the spatial domain corresponds to accentuating high frequencies and hence magnifying noise. This problem is addressed in the Canny and Marr operators by convolving the image with a smoothing operator (Gaussian) before calculating the derivative.