Common Names: Unsharp Filter, Unsharp Sharpening Mask
The unsharp filter is a simple sharpening operator which derives its
name from the fact that it enhances edges (and other high frequency
components in an image) via a procedure which subtracts an unsharp,
or smoothed, version of an image from the original image. The unsharp
filtering technique is commonly used in the photographic and printing
industries for crispening edges.
Unsharp masking produces an edge image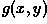 
from
an input image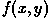 
via
where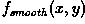 
is a smoothed
version of 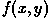. (See Figure 1.)
Figure 1 Spatial sharpening.
We can better understand the operation of the unsharp sharpening filter by examining its frequency response characteristics. If we have a signal as shown in Figure 2(a), subtracting away the lowpass component of that signal (as in Figure 2(b)), yields the highpass, or `edge', representation shown in Figure 2(c).
Figure 2 Calculating an edge image for unsharp filtering.
This edge image can be used for sharpening if we add it back into the original signal, as shown in Figure 3.
Figure 3 Sharpening the original signal using the edge image.
Thus, the complete unsharp sharpening operator is shown in Figure 4.
Figure 4 The complete unsharp filtering operator.
We can now combine all of this into the equation:
where k is a scaling constant. Reasonable values for k vary between 0.2 and 0.7, with the larger values providing increasing amounts of sharpening.
The unsharp filter is implemented as a window-based operator, i.e. it
relies on a
convolution
kernel to perform spatial
filtering. It can be implemented using an appropriately defined
lowpass filter to produce the smoothed version of an
image, which is then pixel subtracted from the original
image in order to produce a description of image edges, i.e. a
highpassed image.
For example, consider the simple image object
whose strong edges have been slightly blurred by camera focus. In order to extract a sharpened view of the edges, we smooth this image using a mean filter (kernel size 3×3) and then subtract the smoothed result from the original image. The resulting image is
(Note, the gradient image contains positive and negative values and, therefore, must be normalized for display purposes.)
Because we subtracted all low frequency components from the original image (i.e., we highpass filtered the image) we are left with only high frequency edge descriptions. Normally, we would require that a sharpening operator give us back our original image with the high frequency components enhanced. In order to achieve this effect, we now add some proportion of this gradient image back onto our original image. The image
has been sharpened according to this formula, where the scaling constant k is set to 0.7.
A more common way of implementing the unsharp mask is by using the negative Laplacian operator to extract the highpass information directly. See Figure 5.
Figure 5 Spatial sharpening, an alternative definition.
Some unsharp masks for producing an edge image of this type are shown in Figure 6. These are simply discrete Laplacian filters. After convolving an original image with a kernel such as one of these, it need only be scaled and and then added to the original.
Figure 6 Three discrete approximations to the Laplacian filter.
With this in mind, we can compare the unsharp and Laplacian of Gaussian filters. First, notice that the gradient images produced by both filters (e.g.
produced by unsharp and
produced by LoG) exhibit the side-effect of ringing, or the introduction of additional intensity image structure. (Note also that the rings have opposite signs due to the difference in signs of the kernels used in each case.) This ringing occurs at high contrast edges. Figure 7 describes how oscillating (i.e. positive, negative, positive, etc.) terms in the output (i.e. ringing) are induced by the oscillating terms in the filter.
Figure 7 Ringing effect introduced by the unsharp mask in the presence of a 2 pixel wide, high intensity stripe. (Gray levels: --1=Dark, 0=Gray, 1=Bright.) a) 1-D input intensity image slice. b) Corresponding 1-D slice through unsharp filter. c) 1-D output intensity image slice.
Another interesting comparison of the two filters can be made by examining their edge enhancement capabilities. Here we begin with reference to
The image
shows the sharpened version produced by a 7×7 Laplacian of Gaussian. The image
is that due to unsharp sharpening with an equivalently sized Laplacian. In comparing the unsharp mask defined using the Laplacian with the LoG, it is obvious that the latter is more robust to noise, as it has been designed explicitly to remove noise before enhancing edges. Note, we can obtain a slightly less noisy, but also less sharp, image using a smaller (i.e. 3×3) Laplacian kernel, as shown in
The unsharp filter is a powerful sharpening operator, but does indeed produce a poor result in the presence of noise. For example, consider
which has been deliberately corrupted by Gaussian noise. (For reference,
is a mean filtered version of this image.) Now compare this with the output of the unsharp filter
and with the original image
The unsharp mask has accentuated the noise.
Adaptive Unsharp Masking
A powerful technique for sharpening images in the presence of low noise levels is via an adaptive filtering algorithm. Here we look at a method of re-defining a highpass filter (such as the one shown in Figure 8) as the sum of a collection of edge directional kernels.
Figure 8 Sharpening filter.
This filter can be re-written as 
times the sum of the eight edge sensitive kernels shown in Figure 9.
Figure 9 Sharpening filter re-defined as eight edge directional kernels
Adaptive filtering using these kernels can be performed by filtering the image with each kernel, in turn, and then summing those outputs that exceed a threshold. As a final step, this result is added to the original image. (See Figure 10.)
Figure 10 Adaptive sharpening.
This use of a threshold makes the filter adaptive in the sense that it overcomes the directionality of any single kernel by combining the results of filtering with a selection of kernels --- each of which is tuned to an edge direction inherent in the image.
You can interactively experiment with this operator by clicking here.
which, after unsharp sharpening (using a mean smoothing filter, with kernel size 3×3) becomes
a) Perform unsharp sharpening on the raw image using a Gaussian filter (with the same kernel size). How do the sharpened images produced by the two different smoothing functions compare? b) Try re-sharpening this image using a filter with larger kernel sizes (e.g. 5×5, 7×7 and 9×9). How does increasing the kernel size affect the result? c) What would you expect to see if the kernel size were allowed to approach the image size?
Notice the effects on features of different scale.
using both the unsharp and Laplacian of Gaussian filters. Which performs best under these conditions?
and
Compare your results with those produced by adaptive unsharp sharpening.
R. Haralick and L. Shapiro Computer and Robot Vision, Addison-Wesley Publishing Company, 1992.
B. Horn Robot Vision, MIT Press, 1986, Chap. 6.
A. Jain Fundamentals of Digital Image Processing, Prentice-Hall, 1989, Chap. 7.
R. Schalkoff Digital Image Processing and Computer Vision, John Wiley & Sons, 1989, Chap. 4.
Specific information about this operator may be found here.
More general advice about the local HIPR installation is available in the Local Information introductory section.
©2003 R. Fisher, S. Perkins,
A. Walker and E. Wolfart.
