ASSEMBLY Reference Frame Calculation Results

The estimation of an ASSEMBLY's reference frame is demonstrated for the robot lower arm.

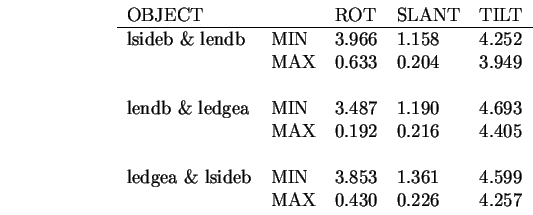
As the rigidly attached hand subcomponent is not visible, it contributes no information. Each of the SURFACEs paired and transformed according to the above theory contributes to these estimates (in the camera coordinate system):

$\begin{displaymath}\vbox{\hskip 1in \begin{tabular}{lllll} OBJECT&& ROT& SLANT&... ... 1.361& 4.599 \\ & MAX& 0.430& 0.226& 4.257 \\ \end{tabular}}\end{displaymath}$

$\begin{displaymath}\vbox{\hskip 1in \begin{tabular}{lllll} & & ROT& SLANT& TILT\... ...& 1.361& 4.693\\ &MAX & 0.192& 0.204 & 3.949\\ \end{tabular}}\end{displaymath}$

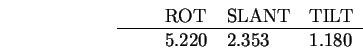
$\begin{displaymath}\vbox{\hskip 1in \begin{tabular}{lllll} && ROT& SLANT& TILT \\ \hline && 5.220 & 2.353& 1.180 \\ \end{tabular}}\end{displaymath}$

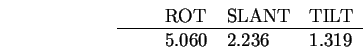
$\begin{displaymath}\vbox{\hskip 1in \begin{tabular}{lllll} && ROT& SLANT& TILT \\ \hline && 5.060& 2.236& 1.319 \\ \end{tabular}}\end{displaymath}$

Translation is estimated after rotation, and starts with an estimate from each individual SURFACE. These estimates are:

$\begin{displaymath}\vbox{\hskip 1in \begin{tabular}{llccc} && X& Y& Z \\ \hline... ...298 & 503. \\ & MAX & 58.116 & 38.875& 592. \\ \end{tabular}}\end{displaymath}$

The translation estimates are integrated by intersection to give the following result:

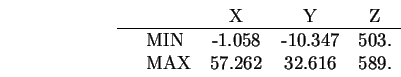
$\begin{displaymath}\vbox{\hskip 1in \begin{tabular}{llccc} & & X &Y& Z \\ \hlin... ....347& 503. \\ &MAX & 57.262 & 32.616& 589. \\ \end{tabular}}\end{displaymath}$

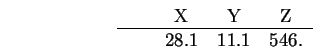
$\begin{displaymath}\vbox{\hskip 1in \begin{tabular}{llccc} && X& Y& Z \\ \hline && 28.1& 11.1& 546. \\ \end{tabular}}\end{displaymath}$

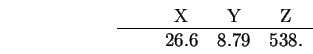
$\begin{displaymath}\vbox{\hskip 1in \begin{tabular}{llccc} && X& Y& Z \\ \hline && 26.6& 8.79& 538. \\ \end{tabular}}\end{displaymath}$

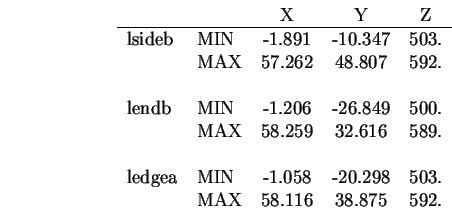
Tables 9.5 and 9.6 summarize the results for the primitive ASSEMBLYs in the test image whose estimates resulted from using more than one SURFACE. The other primitive ASSEMBLYs have reference frames identical to that of the single SURFACE (rotated into the ASSEMBLY's reference frame if necessary). All results are given in the camera coordinate system. The parameter estimates are good, even though both the upper and lower arm are substantially obscured.

**Table 9.5:** Translation Parameters For Primitive ASSEMBLYs
	`Measured (cm)`			`Estimated (cm)`
`ASSEMBLY`	`X`	`Y`	`Z`	`X`	`Y`	`Z`
`robshldbd`	`-13.9`	`17.0`	`558.`	`-15.7`	`11.5`	`562.`
`upperarm`	`0.95`	`26.4`	`568.`	`0.60`	`17.1`	`570.`
`lowerarm`	`26.6`	`8.79`	`538.`	`28.1`	`11.1`	`546.`

**Table 9.6:** Rotation Parameters For Primitive ASSEMBLYs
	`Measured (rad)`			`Estimated (rad)`
`ASSEMBLY`	`ROT`	`SLANT`	`TILT`	`ROT`	`SLANT`	`TILT`
`robshldbd`	`0.257`	`2.23`	`6.12`	`0.135`	`2.30`	`6.28`
`upperarm`	`3.72`	`2.23`	`2.66`	`3.22`	`2.24`	`3.14`
`lowerarm`	`5.06`	`2.23`	`1.32`	`5.22`	`2.35`	`1.18`