Estimating Reference Frames from Previously Recognized Subcomponents

Each previously recognized subcomponent contributes a position estimate. Suppose, the subcomponent has an estimated global reference frame

and the transformation from the subcomponent to the main object is

(given in the model). (If the subcomponent is connected with degrees-of-freedom, then any variables in

will be bound before this step. This is discussed here.) Then, the estimated new global frame is $G_sA^{-1}$ . Figure 9.8 illustrates how the subcomponent's reference frame relates to that of the object.

**Figure 9.8:** *Object and Subcomponent Reference Frame Relationship*
$\begin{figure}\epsfysize =2.7in \epsfbox{FIGURES/Fig9.8.ps}\end{figure}$

In the test image, these ASSEMBLYs had their positions estimated by integrating estimates from subcomponents:

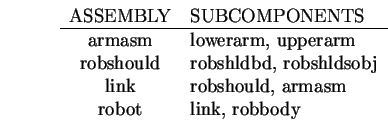
$\begin{displaymath}\vbox{\hskip 0.5in \begin{tabular}{cll} ASSEMBLY& SUBCOMPONE... ...robshould, armasm \\ robot & link, robbody \\ \end{tabular}}\end{displaymath}$

The reference frame estimates for these ASSEMBLYs are summarized in Tables 9.7 and 9.8. Integrating the different position estimates sometimes gives better results and sometimes worse (e.g. robbodyside versus robot rotation). Often, there was little effect (e.g. upperarm versus armasm rotation). A key problem is that transforming the subcomponent's reference frame expands the position estimates so much that it only weakly constrained the ASSEMBLY's reference frame.

**Table 9.7:** Translation Parameters For Structured ASSEMBLYs
`ASSEMBLY`	`X`	`Y`	`Z`	`X`	`Y`	`Z`
	`Measured (cm)`			`Estimated (cm)`
`armasm`	`0.95`	`26.4`	`568.`	`0.60`	`17.1`	`553.`
`robshould`	`-13.9`	`17.0`	`558.`	`-15.7`	`10.3`	`562.`
`link`	`-13.9`	`17.0`	`558.`	`-9.7`	`16.3`	`554.`
`robot`	`-13.8`	`-32.6`	`564.`	`-13.5`	`-35.9`	`562.`

**Table 9.8:** Rotation Parameters For Structured ASSEMBLYs
	`Measured (rad)`			`Estimated (rad)`
`ASSEMBLY`	`ROT`	`SLANT`	`TILT`	`ROT`	`SLANT`	`TILT`
`armasm`	`3.72`	`2.23`	`2.66`	`3.20`	`2.29`	`3.11`
`robshould`	`0.257`	`2.23`	`6.12`	`0.135`	`2.29`	`6.28`
`link`	`0.257`	`2.23`	`6.12`	`0.055`	`2.29`	`0.05`
`robot`	`0.0`	`0.125`	`4.73`	`0.0`	`0.689`	`4.75`

The numerical results for the whole robot in the test scene are summarized in Table 9.9. Here, the values are given in the global reference frame rather than in the camera reference frame.

**Table 9.9:** Measured And Estimated Spatial Parameters
`PARAMETER`	`MEASURED`	`ESTIMATED`
`X`	`488 (cm)`	`486 (cm)`
`Y`	`89 (cm)`	`85 (cm)`
`Z`	`554 (cm)`	`554 (cm)`
`Rotation`	`0.0 (rad)`	`0.07 (rad)`
`Slant`	`0.793 (rad)`	`0.46 (rad)`
`Tilt`	`3.14 (rad)`	`3.53 (rad)`
`Joint 1`	`2.24 (rad)`	`2.18 (rad)`
`Joint 2`	`2.82 (rad)`	`2.79 (rad)`
`Joint 3`	`4.94 (rad)`	`4.56 (rad)`

Better results could probably have been obtained using another geometric estimate integration method (e.g. [63,57]). However, the results here are generally accurate, mainly because of the richness of information in the surface image and geometric object models.