

Next: Stereo matching
Up: Computer Vision IT412
Previous: Motivation
Subsections
Given two images formed in the retinal planes 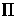 and
and 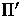 , we want to solve two problems:
, we want to solve two problems:
- For a point m in
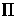 , determine which point
m' in plane
, determine which point
m' in plane 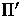 that it corresponds to.
The term correspond
that it corresponds to.
The term correspond![[*]](foot_motif.gif) means that they are the images of the same physical point M.
This is what is commonly known as the
correspondence problem.
means that they are the images of the same physical point M.
This is what is commonly known as the
correspondence problem.
- Given two corresponding points
m and m', compute the 3-D coordinates
of M relative to some global reference frame.
This is known as the reconstruction problem.
This is a special stereo camera configuration
in which
- the two retinal planes are horizontally displaced
and are coplanar in space, and
- the two cameras have identical focal length.
Figure 1:
Disparity and depth measures for parallel cameras (schematic after Faugeras).
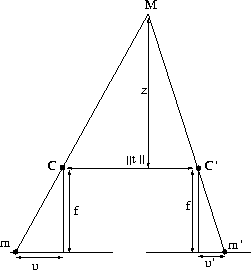 |
Given a scene point M and its
two projection points m of coordinates (u,v)
and m' of coordinates (u',v'),
the disparity value d is defined as
d = u' - u
Note that v = v' as there is no vertical parallax between
the two cameras.
The depth measure z of M is related to
the disparity value d as follows (Fig. 1):
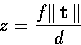
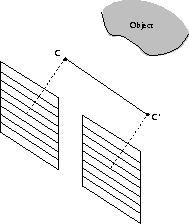
In parallel camera configurations, the epipolar lines coincide with the
horizontal scanlines, and the epipoles are at infinity
(Fig. 2).
As will be seen in Section ![[*]](cross_ref_motif.gif) ,
stereo matching is greatly simplified
for parallel cameras.
,
stereo matching is greatly simplified
for parallel cameras.
Figure 2:
In parallel camera configurations, the epipolar lines are parallel.
 |
Given two corresponding points 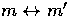 that have coordinates (u,v) and (u',v')
projected by a scene point M
in a general stereo camera configuration, the disparity measure
between m and m' is in fact
a 2-vector instead of a real number. In this case,
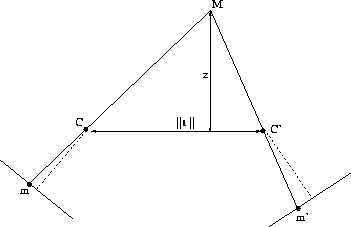
Faugeras (Ch. 6, 1993) chose to define the depth value z
of M as the perpendicular distance of M from the baseline
t and disparity d as a real number that
measures the inverse of z (Fig. 3).
that have coordinates (u,v) and (u',v')
projected by a scene point M
in a general stereo camera configuration, the disparity measure
between m and m' is in fact
a 2-vector instead of a real number. In this case,
Faugeras (Ch. 6, 1993) chose to define the depth value z
of M as the perpendicular distance of M from the baseline
t and disparity d as a real number that
measures the inverse of z (Fig. 3).
Another definition for the depth measure of a scene point
is the z-component of the scene point relative to a
coordinate system fixed at one of the cameras' optical centre.
Figure 3:
A definition of depth measure of a scene point in general stereo
configurations (after Faugeras).
 |
For general stereo configurations, the epipolar lines in
each retinal plane meet at an epipole at a finite distance
(Fig. 4).
Depending on the
orientation of the retinal planes  and
and  relative to the baseline
relative to the baseline 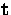 , one of the epipoles
may still be at infinity.
, one of the epipoles
may still be at infinity.
Figure 4:
In general stereo configurations, the epipolar lines in at least
one retinal plane intersect at a point called the epipole
at a finite distance.
 |


Next: Stereo matching
Up: Computer Vision IT412
Previous: Motivation
Robyn Owens
10/29/1997
![[*]](foot_motif.gif) means that they are the images of the same physical point M.
This is what is commonly known as the
correspondence problem.
means that they are the images of the same physical point M.
This is what is commonly known as the
correspondence problem.
![[*]](foot_motif.gif) means that they are the images of the same physical point M.
This is what is commonly known as the
correspondence problem.
means that they are the images of the same physical point M.
This is what is commonly known as the
correspondence problem.
![]()
![[*]](cross_ref_motif.gif) ,
stereo matching is greatly simplified
for parallel cameras.
,
stereo matching is greatly simplified
for parallel cameras.

![]() and
and ![]() relative to the baseline
relative to the baseline ![]() , one of the epipoles
may still be at infinity.
, one of the epipoles
may still be at infinity.
