

Next: Some existing matching algorithms
Up: Computer Vision IT412
Previous: Problem definition
Subsections
Approaches to the correspondence problem can be broadly
classified into two categories: the intensity-based matching
and the feature-based matching techniques.
In the first category, the matching process is applied directly
to the intensity profiles of the two images, while in the
second, features are first extracted from the images and
the matching process is applied to the features.
As shown in the previous section, the epipolar lines
coincide with the horizontal scanlines if the cameras
are parallel, the corresponding points in both images
must therefore lie on the same horizontal scanline.
Such stereo configurations reduce the search for
correspondences from two-dimensions (the entire image)
to one-dimension. In fact, a close look at the intensity
profiles from the corresponding row of the image pair
reveals that the two intensity profiles differ only
by a horizontal shift and a local foreshortening.
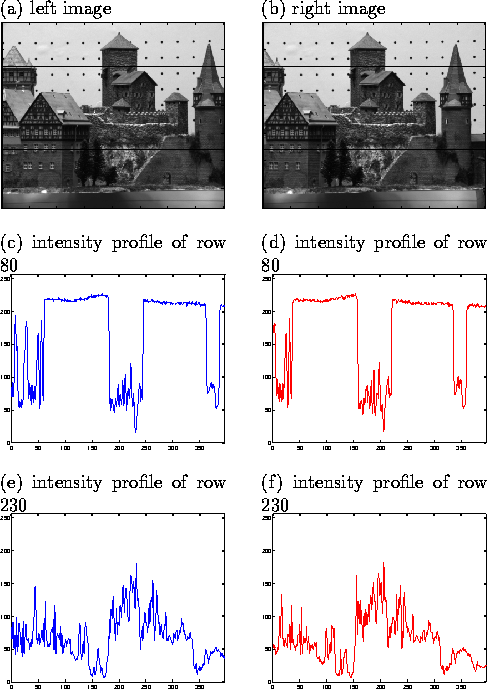
Fig. 5(a) and (b) depict the
images taken with a camera that undergoes a displacement
in the horizontal direction, the image pair therefore corresponds
to a parallel camera set up.
Two black lines are marked at rows 80 and 230 in both images.
Fig. 5(c) and (d), (e) and (f), respectively
show the intensity
profiles of row 80 and row 230 of the two images.
Figure 5:
A comparison of the intensity profiles of two
images from a parallel stereo configuration.
The image pair shown above is retrieved via ftp from
the Calibrated Imaging Laboratory of CMU.
 |
The similarity between the one-dimensional intensity profiles
of the two images suggests an optimization process would be
suitable. Indeed, Barn in 1987 attempted matching
the parallel stereo images using simulated annealing.
He defined an energy function Eij as:
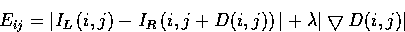
where 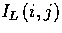 denotes
the intensity value of the left image
at the i-th row and j-th column and
denotes
the intensity value of the left image
at the i-th row and j-th column and
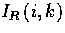 denotes the intensity value
of the right image at
the same row but at the k-th column;
D(i,j) is the disparity value (or horizontal shift
in this case) at the ij-position of the left image.
denotes the intensity value
of the right image at
the same row but at the k-th column;
D(i,j) is the disparity value (or horizontal shift
in this case) at the ij-position of the left image.
The above is clearly a constrained optimization problem in
which the only constraint being used is a minimum change of
disparity values 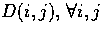 . This constraint
is commonly known as the continuity constraint
(see Section
. This constraint
is commonly known as the continuity constraint
(see Section ![[*]](cross_ref_motif.gif) ).
).
Robe later incorporated the use of a multiresolution scheme
(see Section ![[*]](cross_ref_motif.gif) ) together with a smoothness constraint similar
to that of Barn into the constrained optimization
process. In addition to the horizontal shift of corresponding
pixels, they also allowed the corresponding pixels to undergo vertical
shift (i.e. disparity in the vertical direction), so their
matching method is not restricted to only parallel stereo images.
The energy function to be minimized, as expected, is more complicated
than the one given above.
) together with a smoothness constraint similar
to that of Barn into the constrained optimization
process. In addition to the horizontal shift of corresponding
pixels, they also allowed the corresponding pixels to undergo vertical
shift (i.e. disparity in the vertical direction), so their
matching method is not restricted to only parallel stereo images.
The energy function to be minimized, as expected, is more complicated
than the one given above.
The advantage of this intensity profile matching is that
a dense disparity map and, consequently a dense depth (or range) map,
is output. Unfortunately, like all constrained optimization problems,
whether the system would converge to the global minima is
still an open problem, although, as reported by Robe92,
the multiresolution scheme, to a certain extent, helped
speed up convergence and avoid local minima.
An alternative approach in intensity-based stereo matching,
commonly known as the window-based method, is to
only match those regions in the images that are ``interesting'',
for instance, regions that contain high variation of intensity
values in the horizontal, vertical, and diagonal directions.
The simple Moravec's interest operator (1979)
detects such regions (correspond to regions that have grey-level corners)
from the image pair, and
it has been widely used in many stereo matching systems
(e.g. the SRI STEREOSYS system (Hann, 1985)).
After the interesting regions are detected, a simple
correlation scheme is applied in the matching process;
a match is assigned to
regions that are highly correlated in the two images.
The problem associated with this window-based approach
is that the size of the correlation windows must be
carefully chosen. If the correlation windows are too small,
the intensity variation in the windows will not be
distinctive enough, and many false matches may result.
If they are too large, resolution is lost, since neighbouring
image regions with different disparities will be combined
in the measurement. Worse, the two windows may not
correlate unless the disparity within the windows is
constant, which suggests that the multiresolution scheme
is again appropriate.
Unfortunately, the most serious shortcoming of the window-based approach
-- its sensitivity to the differences in foreshortening --
may sometimes render the approach useless.
Fig. 6 shows a segment MN in the scene
Figure 6:
Foreshortening due to the change of viewing position and
direction.
 |
projecting onto 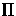 and
and 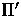 at segments
at segments 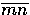 and
and 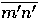 , respectively.
Because of the large difference between the
orientations of the retinal planes and the scene plane,
segment
, respectively.
Because of the large difference between the
orientations of the retinal planes and the scene plane,
segment 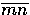 is much
longer than segment
is much
longer than segment 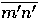 .The windows in the two images
would only give the best correlation measure
if the window used in
.The windows in the two images
would only give the best correlation measure
if the window used in 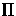 has the size of
has the size of 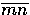 and the window used in
and the window used in 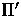 has the size of
has the size of 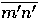 .Such variation of window size to compensate foreshortening
is not possible without
the knowledge of the scene.
This appears to pose a chicken-and-egg problem, since
the whole point is to recover shape using correlation matching.
In the feature-based approach, the image pair is first
preprocessed by an operator so as to extract
the features that are stable under the change
of viewpoint, the matching process is then applied
to the attributes associated with the detected features.
The obvious question here is what type of features that
one should use?
Edge elements, corners, line segments, and curve segments
are features that are robust against the change of perspective,
and they have been widely used in many stereo vision work.
Edge elements and corners
are easy to detect, but may suffer from occlusion;
line and curve segments require extra computation
time, but are more robust against occlusion (they are
longer and so are less likely to be completely occluded). Higher level
image features such as circles, ellipses, and polygonal regions
have also been used as features for stereo matching,
these features are, however, restricted to images of
indoor scenes.
.Such variation of window size to compensate foreshortening
is not possible without
the knowledge of the scene.
This appears to pose a chicken-and-egg problem, since
the whole point is to recover shape using correlation matching.
In the feature-based approach, the image pair is first
preprocessed by an operator so as to extract
the features that are stable under the change
of viewpoint, the matching process is then applied
to the attributes associated with the detected features.
The obvious question here is what type of features that
one should use?
Edge elements, corners, line segments, and curve segments
are features that are robust against the change of perspective,
and they have been widely used in many stereo vision work.
Edge elements and corners
are easy to detect, but may suffer from occlusion;
line and curve segments require extra computation
time, but are more robust against occlusion (they are
longer and so are less likely to be completely occluded). Higher level
image features such as circles, ellipses, and polygonal regions
have also been used as features for stereo matching,
these features are, however, restricted to images of
indoor scenes.
Most feature-based stereo matching systems are
not restricted to using only a specific type of features,
instead, a collection of feature types is incorporated.
For instance, the system proposed by Weng in 1988
combines intensity, edges, and corners to form multiple
attributes for matching; Lim and Binford (1987),
on the other hand, used a hierarchy of features varying from
edges, curves, to surfaces and bodies (2-D regions)
for high-level attribute matching.
- edge elements:
There exist many edge operators for finding
edge elements from an image.
For example, the
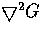 operator followed by a detection of zero-crossings;
the Canny edge detector (1986).
operator followed by a detection of zero-crossings;
the Canny edge detector (1986).
The attributes of edge elements used for matching
can be: coordinates (location in the image),
local orientations (or directions), local intensity profile
on either side of the edge elements
(e.g. from dark to light, or from light to dark).
- corners:
The earliest corner detector is probably
Beaudet's (1978)
rotationally invariant operator called DET;
corner detectors reported in the 80s include
Dreschler and Nagel (1982),
Kitchen and Rosenfeld (1982),
Zuniga and Haralick (1983), etc.
The Harris corner detector (1988)
is one of the popular corner detectors
that are widely used today in Oxford and INRIA.
Attributes of corners that can be used for matching:
coordinates of corners,
type of junctions that the corners correspond to
(e.g. Y-junction, L-function, A-junction, etc.).
- line segments:
To extract line segments from an image, an
edge operator must first be applied.
Line segments are then formed by a linking
and merging operation on the detected edge elements
based on some criteria such as distance, similarity, and
collinearity measures.
Line segment extraction algorithms that have been
reported include:
Nevatia and Babu (1980),
Fischler and Bolles (1983),
Weiss and Boldt (1986).
Attributes of line segments that can be used for matching:
coordinates of end-points, mid-points, orientation
of line segments.
It should be noted that, due to image noise,
the end-points (and thus the mid-points also)
of line segments are normally not reliably
detected, stereo matching process that relies
on the coordinates of these points do not
produce good reconstruction of 3-D coordinates.
In fact, for a pair of matching line segments,
any point on the first line segment can correspond
to every other point on the second line segment,
and this ambiguity can only be resolved if
the end-points of the two line segments are
known exactly.
Using line segments as features for matching
also has the following drawbacks:
- only those line segments that have a
significant difference in direction
with the epipolar lines can be matched.
For line segments whose directions
are close to those of the epipolar lines,
any translation of the line segments
along the line segments' directions
does not cause a significant change to the
epipolar geometry, yet the
subsequent reconstruction process
would be greatly affected.
- for a given line segment in one image,
its corresponding line segment is
likely to be broken into two or
more shorter line segments, thus
the uniqueness constraint
(see Section
![[*]](cross_ref_motif.gif) )
may not be applicable.
)
may not be applicable.
- the reconstruction of 3-D lines
from corresponding 2-D line segments
is not well-defined if the end-points
of the 2-D line segments are not reliable.
This problem can be partially overcome by
incorporating an uncertainty measure
to the 2-D line segments' end-points
as suggested by Zhang (1995).
- curve segments:
The matching of curve segments has not been widely
attempted, the reason is probably due to
the ambiguity involved -- every point on a curve
is likely to be matchable with every other point
on another curve.
Deriche and Faugeras' work (1990)
is one of the very few that has been reported.
They proposed to match the turning points of curves.
- circles, ellipses:
These features are present mainly in indoor scenes
and applicable to detection of defects on industrial parts.
Attributes that can be used for matching: areas in pixel units,
coordinates of the centre of the geometric figures.
- regions:
Regions can be either defined as blobs (e.g. detected
by a region growing algorithm) in the
image or defined as polygonal regions bounded by
line segments.
Regions in the form of blobs have irregular boundary
and may not match perfectly with regions from another image.
For polygonal regions, attributes that can be used for
matching include: areas of regions, bounding line segments
of regions, locations of regions' centroids.
Polygonal regions are very high-level features and could be
costly to extract.
Stereo matching process is a very difficult search procedure.
In order to minimum false matches, some matching constraints
must be imposed. Below is a list of the commonly used constraints.
- Similarity (or compatibility Grimson, 1981).
For the intensity-based approach, the matching pixels
must have similar intensity values (i.e. differ lower than
a specified threshold) or the matching windows must be
highly correlated.
For the feature-based approach, the matching features
must have similar attribute values.
- Uniqueness Marr and Poggio, 1979.
Almost always, a given pixel or feature from one
image can match no more than one pixel or feature
from the other image.
As noted earlier, the uniqueness constraint may not
be applicable to the line segment-based approach.
This constraint can also fail if transparent objects
are present in the scene. Furthermore, given a
pixel or feature m in one image, its ``corresponding''
pixel or feature may be occluded in the other image.
In this case, no match should be assigned to m.
- Continuity Marr and Poggio, 1979.
The cohesiveness of matters suggests that
the disparity of the matches should vary smoothly almost
everywhere over the image.
This constraint fails at discontinuities of depth,
for depth discontinuities cause an abrupt change in
disparity.
- Ordering Baker and Binford, 1981.
If
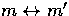 and
and 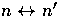 and
if m is to the left of n
then m' should also be to the left of n'
and vice versa. That is, the ordering of features
is preserved across images.
and
if m is to the left of n
then m' should also be to the left of n'
and vice versa. That is, the ordering of features
is preserved across images.
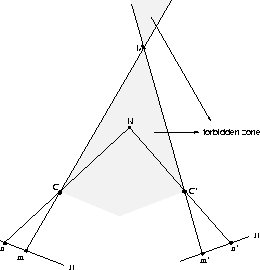
The ordering constraint fails at regions known
as the forbidden zone (Fig. 7).
Figure 7:
The ordering constraint fails if a given 3-D point
(N here) falls onto the forbidden zone of another 3-D point
(M). In the left image (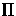 ), m is to the right of n, but
in the right image (
), m is to the right of n, but
in the right image (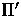 ), this ordering is reversed.
), this ordering is reversed.
 |
- Epipolar.
Given a feature point m in the left image,
the corresponding feature point m' must lie on the
corresponding epipolar line.
This constraint reduces the search space from
two-dimensions to one-dimension. Unlike
all the other constraints, the epipolar constraint
would never fail and could be applied
reliably once the epipolar geometry is known
(this is possible after the fundamental matrix
is estimated, see Appendix B).
By introducing one more camera into the system,
the ambiguity involved in matching can
be further reduced:
Given a feature point 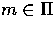 and potential matches
and potential matches 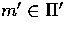 and
and 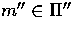 , an epipolar line
, an epipolar line 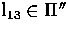 can be constructed
using m and the epipolar geometry between
can be constructed
using m and the epipolar geometry between 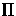 and
and 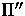 , another epipolar line
, another epipolar line 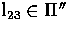 can also be constructed
using m' and the epipolar geometry between
can also be constructed
using m' and the epipolar geometry between 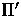 and
and 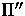 . The two epipolar lines
. The two epipolar lines 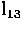 and
and 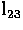 must intersect at m'' if
must intersect at m'' if
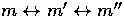 .
.
- Relaxation.
A global matching constraint to eliminate false matches.
An example (Barnard and Thompson, (1980))
of applying relaxation to stereo matching:
assign to each candidate match a probability value
based on some criteria on the ``goodness of match'';
iteratively update this probability value for
each candidate match; finally, delete those matches
whose probability value is below a certain threshold.
The update process in each iteration is as follows:
increase probability of a given candidate match 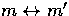 by a value that is proportional
to the number of neighbouring matches that have
consistent disparity values with
by a value that is proportional
to the number of neighbouring matches that have
consistent disparity values with 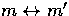 .
.
Other criteria may also be used in the update process,
e.g. the geometric support as proposed by
Ayache and Faverjon (1987).
The coarse-to-fine multiresolution matching scheme
works as follows:
- generate a pair of image pyramids (a hierarchy of images)
from the original image pair so that
only few and prominent features are
present at the coarse levels.
The original images are at the finest level
of the image pyramids.
- start the matching process at the coarsest level.
- use the matches obtained at the coarser
level to guide the matching process
gradually up to the finest level.
Figure 8:
By applying to an image Laplacian of Gaussian filters
of different 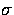 values followed by a detection
of zero-crossings, a hierarchy of edge map from
coarse to fine levels can be obtained.
values followed by a detection
of zero-crossings, a hierarchy of edge map from
coarse to fine levels can be obtained.
 |
An image pyramid of edges can be obtained by convolving the images
with a Laplacian of Gaussian filter of different widths (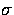 )followed by a detection of zero-crossings (Fig. 8).
An image pyramid of grey level images can be obtained
by applying a smoothing operation followed by sub-sampling
(i.e. reducing the image resolution by a factor of 2).
Such image pyramid is sometimes referred to as the processing cone
(Fig. 9).
The SRI STEREOSYS system described later used this
smooth and sub-sample scheme.
)followed by a detection of zero-crossings (Fig. 8).
An image pyramid of grey level images can be obtained
by applying a smoothing operation followed by sub-sampling
(i.e. reducing the image resolution by a factor of 2).
Such image pyramid is sometimes referred to as the processing cone
(Fig. 9).
The SRI STEREOSYS system described later used this
smooth and sub-sample scheme.
Figure 9:
Processing cone.
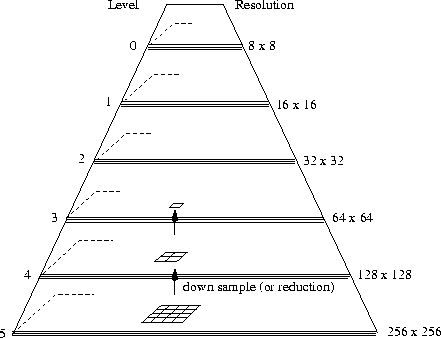 |


Next: Some existing matching algorithms
Up: Computer Vision IT412
Previous: Problem definition
Robyn Owens
10/29/1997


![]()
![]() . This constraint
is commonly known as the continuity constraint
(see Section
. This constraint
is commonly known as the continuity constraint
(see Section ![[*]](cross_ref_motif.gif) ).
).
![[*]](cross_ref_motif.gif) ) together with a smoothness constraint similar
to that of Barn into the constrained optimization
process. In addition to the horizontal shift of corresponding
pixels, they also allowed the corresponding pixels to undergo vertical
shift (i.e. disparity in the vertical direction), so their
matching method is not restricted to only parallel stereo images.
The energy function to be minimized, as expected, is more complicated
than the one given above.
) together with a smoothness constraint similar
to that of Barn into the constrained optimization
process. In addition to the horizontal shift of corresponding
pixels, they also allowed the corresponding pixels to undergo vertical
shift (i.e. disparity in the vertical direction), so their
matching method is not restricted to only parallel stereo images.
The energy function to be minimized, as expected, is more complicated
than the one given above.
![[*]](cross_ref_motif.gif) )
may not be applicable.
)
may not be applicable.

![]() and potential matches
and potential matches ![]() and
and ![]() , an epipolar line
, an epipolar line ![]() can be constructed
using m and the epipolar geometry between
can be constructed
using m and the epipolar geometry between ![]() and
and ![]() , another epipolar line
, another epipolar line ![]() can also be constructed
using m' and the epipolar geometry between
can also be constructed
using m' and the epipolar geometry between ![]() and
and ![]() . The two epipolar lines
. The two epipolar lines ![]() and
and ![]() must intersect at m'' if
must intersect at m'' if
![]() .
.![]() by a value that is proportional
to the number of neighbouring matches that have
consistent disparity values with
by a value that is proportional
to the number of neighbouring matches that have
consistent disparity values with ![]() .
.
![]() )followed by a detection of zero-crossings (Fig. 8).
An image pyramid of grey level images can be obtained
by applying a smoothing operation followed by sub-sampling
(i.e. reducing the image resolution by a factor of 2).
Such image pyramid is sometimes referred to as the processing cone
(Fig. 9).
The SRI STEREOSYS system described later used this
smooth and sub-sample scheme.
)followed by a detection of zero-crossings (Fig. 8).
An image pyramid of grey level images can be obtained
by applying a smoothing operation followed by sub-sampling
(i.e. reducing the image resolution by a factor of 2).
Such image pyramid is sometimes referred to as the processing cone
(Fig. 9).
The SRI STEREOSYS system described later used this
smooth and sub-sample scheme.