The evolution of the mesh can be controlled by assigning an equation of motion to each mexel. In the general case the equation of motion is Newtonian:
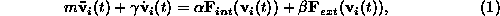
where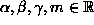 
and t is time. The
purpose of the internal force 
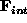is impose image
independent soft constraints on the shape of the mesh to guarantee
e.g. smoothness of the resulting surface mesh. The external force
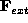draws the mesh towards salient image features.
In discrete form (1) is written as (assuming m = 1)
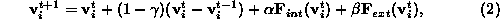
with the initial mesh when time t = 0 given.
When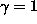 
, (2) reduces to a Lagrangian equation of motion. A
simple internal force can be defined as
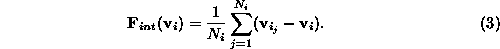
The internal force (3) causes
surface to shrink to a point if no external force is present. This
is sometimes useful, because it reduces sensitivity to the initialization
provided that initial meshes are set outside
the target.
Semi-implicit evolution equations, such as in snakes [3], are not popular with 3-D meshes. This is since in the 3-D case this involves multiplication of large matrices, which do not have a banded structure as in the 2-D case.
The formulation of external forces is difficult because they should
guide the surface mesh to a good representation of the target
surface. A basic external force can be defined as
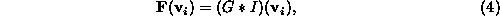
where * is the convolution operator, G is a Gaussian kernel and
I is the input image, which is appropriately scaled version of the
pre-processed original image. Pre-processing can be,
for example, edge-detection. More advanced (and useful) solutions for
constructing external forces based on the image data are given in
[16], [15] and [1].