From Quadtrees to Dynamic Trees
Dynamic trees have grown up in response to the problems of image segmentation. The underlying need is one of building models of images. Traditional modelling techniques tend to be non-probabilistic, and therefore somewhat ad-hoc, although reasonable performance can be achieved if the methods accurately represent image structure. Probabilistic models often take the form of Markov random fields. These have a flat structure, and although they capture some of the local coherence of the image, they have no hierarchical structure. Tree based structures promise to provide that hierarchy, and at the same time may well enable the concept of an object to be captured in some form.
Probabilistic quadtree models (a two dimensional version of the binary
tree) were developed by Chris Williams and Xiaojuan Feng. The leaf nodes of the
quadtree represent the local class labels of the image (for
segmentation). The probabilistic map from the leaf node classes to the image
pixels was modelled using a neural network. The adjacent diagram shows
the form of a binary tree.
Quadtrees have the advantage of their tree structure. Belief propagation can be used to obtain the marginal probabilities of each node given the data, and to obtain the likelihood of the tree. Practical results on real segmentation problems have been reasonable. Their main disadvantage is their fixed structure. Quadtrees produce blocky artefacts in their segmentation due to the fact that two (spatially) adjacent leaf nodes might only be path connected through a vertex far up the tree hierarchy.
One way around this type of problem is to use dynamic trees (see the
diagram below). This is a mixture of tree structures formed by
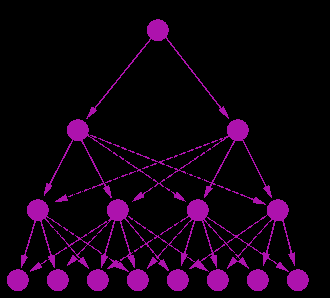allowing each vertex to `choose' its parent. This reduces the blockiness problem
of the quadtree, because any two leaf nodes can be connected at any level of hierarchy.
Dynamic tree models are in fact tree mixtures, and because the number of trees in the mixture grows exponentially with
network size, exact belief propagation becomes intractable. We have to
resort to the approximation techniques outlined earlier. I have been
pursuing work on this in collaboration with Chris Williams, Stephen Felderhof and Nick Adams.
