Motivation
When tackling large multivariate, high dimensional problems, the Bayesian approach has inherited certain structural elements from both the neural networks field and the maximum likelihood method. It is common to characterise Bayesian modelling as involving certain steps:
- Finding a sensible (or versatile) deterministic model for the variables of interest. This might be a neural network model, a linear model, a generalised linear model, a radial basis model or whatever.
- Postulating some stochastic deviation from the deterministic model, often called an error model.
- Summoning forth Bayes, and claiming the right to call the parameters of the model, `random variables'.
- Postulating some prior probability distribution over those parameters. This distribution might in turn have `hyperparameters' which should also have a distribution, and so on.
This view of the Bayesian approach is anaemic. There is no need to work with deterministic models at all; sometimes they are not the most appropriate. It also separates (as is very common) the model and the prior. It should never be forgotten that the choice of models is often a much stricter specification of prior information than the prior distribution over the parameters of those models.
One of the common application areas of neural network-type models is with a nonlinear regression problem. The neural network is used to model the function from the independent variables (input space) to the dependent variables (output space). Why are neural networks used? Not because they represent, in any way, the prior information about the expected shape of the regression function. Rather it is because the class of neural networks are general approximators, and so big enough networks will include possible functions very close to any other function.
This is not a Bayesian way of thinking. General approximation on its own is not useful. It enables the modelling function to fit the data exactly, including all the errors. In order to put this into a Bayesian framework, prior distributions should be put over the parameters of the neural network. But the neural network functions were not chosen to have any particular meaning anyway. How then can the prior distributions over the parameters of the network be chosen to accurately represent the prior beliefs about the functions? Understandably, this is not straightforward. Certain regularisation-like methods can be used to allow the prior over parameters to favour smoother functions. But is this the best way of going about it?
Suppose instead that we focus on the prior information which we have. With regression we are usually talking about smoothness and scaling information. One good way of representing such information is in terms of local smoothness. This can be defined directly in probabilistic terms through the use of the concept of a process. Gaussian processes are one of the simplest types of random processes, and have many features which are very useful in Bayesian modelling.
Instead of specifying a set of deterministic functions, and then
putting a probability distribution over those functions, we can define
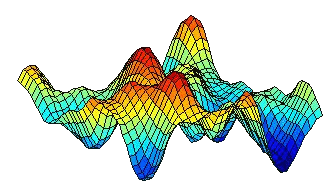the prior all at once by using a random process. With a Gaussian
process, the prior is determined by a covariance function which
represents the smoothness of the process. An example of a sample from
a Gaussian process (with a squared exponential covariance function) is
illustrated.
The great benefit of Gaussian processes is that the marginal distribution over function values at any finite set of points can be specified, and is Gaussian. This enables us to only focus on the variables of interest. A few topics of older work are listed below
Toeplitz methods and Gaussian processes
Certain types of problems allow the structure of the covariance matrix to be utilised to improve performance.
Modelling switching between regimes
Gaussian processes are generally applied to stationary problems. One common non-stationary problem involves switching processes.
