This page describes the Bayesian Fourier Transform. Quicklinks to the code will soon be available. Demos of the application of the method to some audio data is available on the Bayesian Fourier Transform Demos page.
The fast Fourier transform (FFT) is a fundamental component in any numerical toolbox. There are many circumstances where Fourier analysis would be useful when there is missing or irregularly sampled data or uncertainty in the data. The following scenarios are just some in which these problems might occur.
- There is temporary/regular instrument failure or interruption.
- There are scratches on media, such as compact disks.
- Missing packets occur in streamed data.
- Data is not a power of two in length or we have irregularly shaped image patches.
- Data is quantised, either in Fourier domain (e.g. jpeg) or data domain (e.g. integer storage).
Prior information is needed to infer the missing data or the corresponding Fourier components. However to be practically useful inference must be fast. Ideally we want techniques which are near to O(n log n).
The Fast Fourier Transform can be represented graphically (See eg Aji and McEliece 2000). This graphical representation can be thought of as a deterministic belief network. To draw the network simply it is best to view the data in bit-reversed order (for example data in position with binary representation 0001001 is put in position 1001000). Then the network can be viewed in the form below.
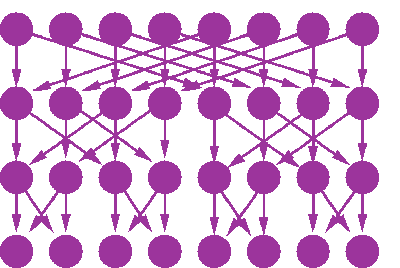
In this figure, the top row denotes the Fourier components and the bottom row denotes the data. This can be thought of as a generative model of the data given the Fourier components. By specifying a prior distribution for the Fourier components, we can utilise the FFT graphical model in situations when the data is not entirely known. It might be that some data is missing, or there is some other error in the data.
There is still the question as to what prior to give for the Fourier components. For now we consider the simplest of these priors - independent complex Gaussians on each component. We are free to specify the means and variances of those Gaussians. In general, we will probably know little about the phase of any component, and so it is reasonable to presume a zero mean. However the variances will depend on the prior belief we have regarding the spectral characteristics of the signal.
Inference in the FFT network is not trivial. The network is multiply connected, and the loops are actually quite tight. If we moralise the network we get a Markov network of the form
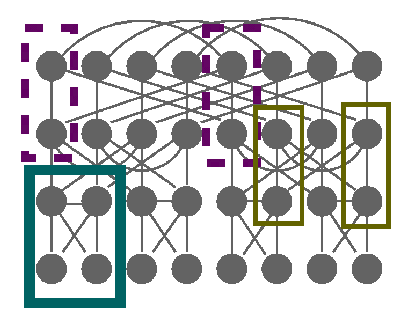
There are a number of approaches we can take to inference in this network.
- Form the full joint Gaussian and condition on the known data.
- Calculate the inverse covariance of the full Gaussian, and use the partitioned inverse equations to obtain the covariance for the known data. This can then be used to calculate the means of the unknown data.
- Use mean field methods to obtain approximate distributions for the missing data and the Fourier components.
- Use loopy belief propagation to obtain approximate distributions for the missing data and the Fourier components.
- Use generalised belief propagation to obtain approximate distributions for the missing data and the Fourier components.
- Use clustered mean field methods.
We will consider all the options other than the last one, which though an entirely valid possibility, has not yet been covered.