






Common Names: Crimmins Speckle Removal
Crimmins Speckle Removal  reduces speckle
from an image using the Crimmins
complementary hulling algorithm. The algorithm has been
specifically designed to reduce the intensity of salt and
pepper noise in an image. Increased iterations of the algorithm yield
increased levels of noise removal, but also introduce a significant
amount of blurring of high frequency details.
reduces speckle
from an image using the Crimmins
complementary hulling algorithm. The algorithm has been
specifically designed to reduce the intensity of salt and
pepper noise in an image. Increased iterations of the algorithm yield
increased levels of noise removal, but also introduce a significant
amount of blurring of high frequency details.
Crimmins Speckle Removal works by passing an image through a speckle removing filter which uses the complementary hulling technique (raising pixels that are darker than their surrounding neighbors, then complementarily lowering pixels that are brighter than their surrounding neighbors) to reduce the speckle index of that image. The algorithm uses a non-linear noise reduction technique which compares the intensity of each pixel in an image with those of its 8 nearest neighbors and, based upon the relative values, increments or decrements the value of the pixel in question such that it becomes more representative of its surroundings. The noisy pixel alteration (and detection) procedure used by Crimmins is more complicated than the ranking procedure used by the non-linear median filter. It involves a series of pairwise operations in which the value of the `middle' pixel within each neighborhood window is compared, in turn, with each set of neighbors (N-S, E-W, NW-SE, NE-SW) in a search for intensity spikes.
The operator has a simple form. Suppose that at any time the three consecutive pixels (e.g. on a N-S column) that are being examined are a, b, c. The algorithm is:
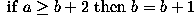
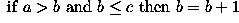
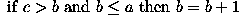
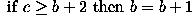

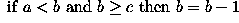
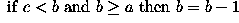
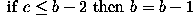
Note that, over several iterations, the effects of smoothing in this way propagate out from the intensity spike to infect neighboring pixels. In other words, the algorithm smoothes by reducing the magnitude of a locally inconsistent pixel, as well as increasing the magnitude of pixels in the neighborhood surrounding the spike. It is important to notice that a spike is defined here as a pixel whose value is more than 2 intensity levels different from its surroundings. This means that after 2 iterations of the algorithm, the immediate neighbors of such a spike may themselves become spikes with respect to pixels lying in a wider neighborhood.
We begin examining the Crimmins Speckle Removal algorithm using the image
which is a contrast-stretched version of
We can corrupt this image with a small amount (i.e. p=0.1% that a bit is flipped) of salt and pepper noise
and then use several iterations of the Crimmins Speckle Removal algorithm to clean it up. The results after 1, 4 and 8 iterations of the algorithm are:
It took 8 iterations to produce the relatively noise-free version that is shown in the latter image.
In this case, it is instructive to examine the images where significant noise still exists. For example, we can quantify what we see qualitatively (that the intensity of the speckle noise is decreasing with increased iterations of the algorithm) by measuring the intensity values of a particular (arbitrarily chosen) noisy pixel in each of the noisy images. If we zoom a small portion of (i) the original noisy corrupted image
(ii) the speckle filtered image after 1 iteration
and (iii) 4 iterations
we find that the pepper intensity spike just under the eye takes on intensity values 51, 67, and 115 respectively. This confirms what we would expect from an algorithmic analysis: each iteration of Crimmins Speckle Removal reduces the magnitude of a noise spike by 16 intensity levels (2 for each of 8 neighbor directions).
We can also see from this example that a noisy spike (i.e. any pixel whose magnitude is different than its neighbors by more than 2 levels) is reduced by driving its pixel intensity value towards those of its neighbors and driving the neighboring values towards that of the spike (although the latter phenomena occurs rather more slowly). By increasing the number of iterations of the algorithm, we increase the extent of this effect, and hence, incur blurring. (If we keep increasing the number of iterations, we would obtain an image with very little contrast, as all sharp gradients will be smoothed down to a magnitude of 2 intensity levels.)
An extreme example of this can be demonstrated using the image
which has been corrupted by p=1% (that a bit is flipped) salt and pepper noise. The original is
In order to remove all the noise, as shown in
13 iterations of Crimmins Speckle Removal are required. Much detail has been sacrificed. We can obtain better performance out of Crimmins Speckle Removal if we use fewer iterations of the algorithm. However, because this algorithm reduces noise spikes by a few intensity levels at each iteration, we can only expect to remove noise over few iterations if the noise has a similar intensity value(s) to those of the underlying image. For example, applying 8 iterations of Crimmins Speckle Removal to the face corrupted with 5% salt noise, as shown in
yields
Here the snow has been removed from the light regions on the subject's face and sweater, but remains in areas where the background is dark.
The foregoing discussion has pointed to the fact that the Crimmins
Speckle Removal algorithm is most useful on images corrupted by noise
whose values are not more than a couple intensity levels different
from those in the underlying image. For example, we can use Crimmins
to smooth the Gaussian noise corrupted image (zero mean
and 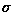 =8)
=8)
The result, after only 2 iterations, is shown in
Below results are tabulated for other smoothing operators applied to this noisy image.
The results of filtering this image are given below:
smoothed with a 3×3 kernel mean filter,
smoothed with a 5×5 kernel mean filter,
smoothed with a 5×5 kernel Gaussian smoothing filter,
smoothed with a 3×3 kernel median filter,
If we allow a little noise in the output of the Crimmins filter (though not as much as we see in some of the above filter outputs), we can retain a good amount of detail, as shown in
This used a single application of the operator. If you now return to examine the cropped and zoomed versions of the first series of examples in this worksheet, you can see the Gaussian noise components being smoothed away after very few iterations (i.e. long before the more dramatic noise spikes are reduced).
You can interactively experiment with this operator by clicking here.
which has poor contrast and a limited dynamic range centered in the middle of the grayscale spectrum. First filter a p=3% salt and peppered version of this image. Then take the resultant image and contrast stretch it using a cutoff frequency of 0.03. Compare your result to
which was filtered (and noise corrupted, using p=3%) after contrast stretching. It took 11 iterations to produce the latter. Why did it take fewer filtering iterations to remove the noise in your result? Why doesn't your result look as good?
with Gaussian noise
with a large 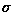 and then filter it using Crimmins
Speckle removal. Compare your results with that achieved by
mean filtering, median filtering, and
conservative smoothing.
and then filter it using Crimmins
Speckle removal. Compare your results with that achieved by
mean filtering, median filtering, and
conservative smoothing.
T. Crimmins The Geometric Filter for Speckle Reduction, Applied Optics, Vol. 24, No. 10, 15 May 1985.
Specific information about this operator may be found here.
More general advice about the local HIPR installation is available in the Local Information introductory section.



