Common Names: Frequency Filters
Frequency filters process an image in the frequency domain. The image
is Fourier transformed, multiplied with the filter
function and then re-transformed into the spatial domain. Attenuating
high frequencies results in a smoother image in the spatial domain,
attenuating low frequencies enhances the edges.
All frequency filters can also be implemented in the spatial domain and, if there exists a simple kernel for the desired filter effect, it is computationally less expensive to perform the filtering in the spatial domain. Frequency filtering is more appropriate if no straightforward kernel can be found in the spatial domain, and may also be more efficient.
Frequency filtering is based on the Fourier Transform. (For the following discussion we assume some knowledge about the Fourier Transform, therefore it is advantageous if you have already read the corresponding worksheet.) The operator usually takes an image and a filter function in the Fourier domain. This image is then multiplied with the filter function in a pixel-by-pixel fashion:
where F(k,l) is the input image in the Fourier domain, H(k,l) the filter function and G(k,l) is the filtered image. To obtain the resulting image in the spatial domain, G(k,l) has to be re-transformed using the inverse Fourier Transform.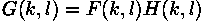
Since the multiplication in the Fourier space is identical to convolution in the spatial domain, all frequency filters can in theory be implemented as a spatial filter. However, in practice, the Fourier domain filter function can only be approximated by the filtering kernel in spatial domain.
The form of the filter function determines the effects of the
operator. There are basically three different kinds of filters:
lowpass,
highpass and
bandpass
filters. A low-pass
filter attenuates high frequencies and retains low frequencies
unchanged. The result in the spatial domain is equivalent to that of a
smoothing filter; as the blocked high frequencies
correspond to sharp intensity changes, i.e. to the fine-scale details
and noise in the spatial domain image.
A highpass filter, on the other
hand, yields edge enhancement or edge detection in the spatial domain,
because edges contain many high frequencies. Areas of rather constant
graylevel consist of mainly low frequencies and are therefore
suppressed.
A bandpass attenuates very low and very high
frequencies, but retains a middle range band of frequencies. Bandpass
filtering can be used to enhance edges (suppressing low
frequencies) while reducing the noise at the same time (attenuating
high frequencies).
The most simple lowpass filter is the ideal lowpass. It
suppresses all frequencies higher than the cut-off frequency
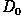and leaves smaller frequencies unchanged:
In most implementations, 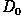is given as a fraction
of the highest frequency represented in the Fourier domain image.
The drawback of this filter function is a ringing
effect that occurs
along the edges of the filtered spatial domain image. This phenomenon is
illustrated in Figure 1, which shows the shape of the
one-dimensional filter in both the frequency and spatial domains for two
different values of 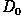. We obtain the shape of the
two-dimensional filter by rotating these functions about the
y-axis. As mentioned earlier, multiplication in the Fourier
domain corresponds to a convolution in the spatial domain. Due to the
multiple peaks of the ideal filter in the spatial domain, the filtered
image produces ringing along intensity edges in the spatial domain.
Figure 1 Ideal lowpass in frequency and spatial domain.
Better results can be achieved with a Gaussian shaped filter function. The advantage is that the Gaussian has the same shape in the spatial and Fourier domains and therefore does not incur the ringing effect in the spatial domain of the filtered image. A commonly used discrete approximation to the Gaussian is the Butterworth filter. Applying this filter in the frequency domain shows a similar result to the Gaussian smoothing in the spatial domain. One difference is that the computational cost of the spatial filter increases with the standard deviation (i.e. with the size of the filter kernel), whereas the costs for a frequency filter are independent of the filter function. Hence, the spatial Gaussian filter is more appropriate for narrow lowpass filters, while the Butterworth filter is a better implementation for wide lowpass filters.
The same principles apply to highpass filters. We obtain a highpass
filter function by inverting the corresponding lowpass filter, e.g. an
ideal highpass filter blocks all frequencies smaller than
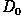and leaves the others unchanged.
Bandpass filters are a combination of both lowpass and highpass
filters. They attenuate all frequencies smaller than a frequency
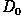and higher than a frequency
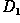, while the frequencies between the two cut-offs
remain in the resulting output image. We obtain the filter function of
a bandpass by multiplying the filter functions of a lowpass and of a
highpass in the frequency domain, where the cut-off frequency of the
lowpass is higher than that of the highpass.
Instead of using one of the standard filter functions, we can also create our own filter mask, thus enhancing or suppressing only certain frequencies. In this way we could, for example, remove periodic patterns with a certain direction in the resulting spatial domain image.
Frequency domain filters are most commonly used as lowpass filters. We will demonstrate this performance with
Corrupting this image with Gaussian noise with a zero mean and a standard deviation of 8 yields
We can reduce this type of noise using a lowpass filter, because noise consists largely of high frequencies, which are attenuated by a lowpass filter.
The image
is the result of applying an ideal lowpass filter to
the noisy image with the cut-off frequency being
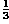. Although we managed to reduce the high
frequency noise, this image is of no practical use. We lost too many of
the fine-scale details and the image exhibits strong ringing due to the
shape of the ideal low pass filter.
Applying the same filter with a cut-off frequency of 0.5 yields
Since this filter keeps a greater number of frequencies, more details remain in the output image. The image is less blurred, but also contains more noise. The ringing is less severe, but still exists.
Better results can be achieved with a Butterworth filter. We obtain
with a cut-off frequency of 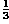. This image doesn't show any visible ringing and only little noise. However, it also lost some image information, i.e. the edges are blurred and the image contains less details than the original.
In order to retain more details, we increase the cut-off frequency to 0.5, as can be seen in
This image is less blurred, but also contains a reasonable amount of noise. In general, when using a lowpass filter to reduce the high frequency noise, we have to compromise some desirable high frequency information if we want to smooth away significant amounts of noise.
The ringing effect originating from the shape of the ideal lowpass can be better illustrated using the following artificial image. The image
is a binary image of a rectangle. Filtering
this image with an ideal lowpass filter (cut-off frequency
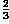) yields
The ringing is already recognizable in this image but is much more obvious in
which is obtained after a histogram equalization. The effect gets even worse if we block more of the frequencies contained in the input image. In order to obtain
we used a cut-off frequency of
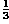. Apart from the (desired) smoothing the
image also contains a severe ringing which clearly visible even
without histogram equalization. We can also see that the cut-off
frequency directly corresponds to the frequency of the ringing, i.e. as
we double the cut-off frequency, we double the distance between two
rings. The image
has been filtered with a
Butterworth filter using a cut-off frequency of
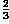. In contrast to the above examples, this
image doesn't exhibit any ringing.
We will illustrate the effects of highpass frequency filtering using
as well. As a result of attenuating (or blocking) the low frequencies, areas of constant intensity in the input image are zero in the output of the highpass filter. Areas of a strong intensity gradient, containing the high frequencies, have positive and negative intensity values in the filter output. In order to display the image on the screen, an offset is added to the output in the spatial domain and the image intensities are scaled. This results in a middle grayvalue for low frequency areas and dark and light values for the edges. The image
shows the output of a Butterworth highpass with the cut-off frequency being 0.5. An alternative way to display the filter output is to take the absolute value of the filtered spatial domain image. If we apply this method to the clown image (and threshold the result with 13) we obtain
This image may be compared with
which is an edge image produced by the Sobel operator and, thus, shows the absolute value of the edge magnitude. We can see that the Sobel operator detects the edges better than the highpass filter. In general, spatial filters are more commonly used for edge detection while frequency filters are more often used for high frequency emphasis. Here, the filter doesn't totally block low frequencies, but magnifies high frequencies relative to low frequencies. This technique is used in the printing industries to crispen image edges.
Frequency filters are quite useful when processing parts of an image which can be associated with certain frequencies. For example, in
each part of the house is made of stripes of a different frequency and orientation. The corresponding Fourier Transform (after histogram equalization can be seen in
We can see the main peaks in the image corresponding to the periodic patterns in the spatial domain image which now can be accessed separately. For example, we can smooth the vertical stripes (i.e. those components which make up the wall in the spatial domain image) by multiplying the Fourier image with the frequency mask
The effect is that all frequencies within the black rectangle are set to zero, the others remain unchanged. Applying the inverse Fourier Transform and normalizing the resulting image yields
in the spatial domain. Although the image shows some regular patterns in the formerly constant background, the vertical stripes are almost totally removed whereas the other patterns remained mostly unchanged.
We can also use frequency filtering to achieve the opposite effect, i.e. finding all features in the image with certain characteristics in the frequency domain. For example, if we want to keep the vertical stripes (i.e. the wall) in the above image, we can use
as a mask. To perform the frequency filtering we transform both the image of the house and the mask into the Fourier domain where we multiply the two images with the effect that the frequencies occurring in the mask remain in the output while the others are set to zero. Re-transforming the output into the spatial domain and normalizing it yields
In this image, the dominant pattern is the one defined by the mask. The pixel values are the highest at places which were composed of this vertical pattern in the input image and are zero in most of the background areas. It is now possible to identify the desired area by applying a threshold, as can be seen in
To understand this process we should keep in mind that a multiplication in the Fourier domain is identical to a convolution in the spatial domain.
Frequency filters are also commonly used in
image reconstruction.
Here, the aim is to remove the effects of a non-ideal
imaging system by multiplying the image in the Fourier space with an
appropriate function. The easiest method, called inverse filtering, is
to divide the image in the Fourier space with the optical transfer
function (OTF). We illustrate this technique, also known as
deconvolution,
using
We simulate a non-ideal OTF by multiplying the Fourier Transform of the image with the Fourier Transform of a Gaussian image with a standard deviation of 5. Re-transforming the result into the spatial domain yields the blurred image
We can now reconstruct the original image using inverse filtering by taking the Fourier Transform of the blurred image and dividing it by the Fourier Transform of the Gaussian kernel, which was used to initially blur the image. The reconstructed image is shown in
Although we obtain, in the above case, exactly the original image, this method has two major problems. First, it is very sensitive to noise. If we, for example, add 0.1% spike noise to the blurred image, we obtain
Inverse filtering the image (as described above) using this image in order to de-blur yields the low contrast result
(Note that doing contrast enhancement to emphasize the original image features can produce an image very similar to the original, except for a loss of fine details). The situation can be slightly improved if we ignore all values of the Fourier space division in which the divisor (i.e. the value of the OTF) is below a certain threshold. The effect of using a threshold of 3 can be seen in
However, if we increase the threshold we have to discard more of the Fourier values and therefore lose more image information. Hence, we will be less successful in reconstructing the original image.
The second problem with this image restoration method is that we need to know the OTF which corrupted the image in the first place. If we, for example, blur the image by convolving it with the Gaussian image in the spatial domain, we obtain
Although this should theoretically be the same image as obtained from the multiplication in the Fourier Space, we obtain small differences due to quantization errors and effects around the border of an image when convolving it in spatial domain. Reconstructing the original image by dividing the blurred image in the Fourier space with the Fourier Transform of the Gaussian yields
or
if we use a minimum OTF threshold of 5.
We face a similar problem if we want to deconvolve a real blurred image like
Since we do not know the transfer function which caused the blurring, we have to estimate it. The images
and
are the results of estimating the OTF with a Gaussian image with a standard deviation of 3 and 10, respectively and applying an inverse filtering with a minimum OTF threshold of 10. We can see that the image improved only very little, if at all.
Due to the above problems, in most practical cases more sophisticated
reconstruction methods are used. For example, Wiener filtering
and Maximum Entropy filtering
are two techniques that are based
on the same principle as inverse filtering, but produce better results
on real world images.
Finally, frequency filtering can also be used for
pattern matching.
For example, we might want to find all locations in
which are occupied by a certain letter, say X. To do this, we need an image of an isolated X which can act as a mask, in this case
To perform the pattern matching, we transform both image and mask into the Fourier space and multiply them. We apply the inverse Fourier Transform to the resulting Fourier image and scale the output to obtain
in the spatial domain. This image is (theoretically) identical to the result of convolving image and mask in the spatial domain. Hence, the image shows high values at locations in the image which match the mask well. However, apart from the X, these are also other letters like the R and the K which match well. In fact, if we threshold the image at 255, as can be seen in
) we have two locations indicating an X, one of them being incorrect.
Since we multiplied the two complex Fourier images, we also changed the phase of the original text image. This results in a constant shift between the position of the letter in the original and its response in the processed image. The example shows that this straightforward method runs into problems if we want to distinguish between similar patterns or if the mask and the corresponding pattern in the data differ slightly. Another problem includes the fact that this operation is neither rotation- nor scale-invariant. (Note that we also run into these problems if we implement the operation as a simple convolution in the spatial domain.) The size of the pattern determines whether it is better to perform the matching in the spatial or frequency domain. In our case (the letter was approximately 10×20 pixels); it is substantially faster to do the matching in the frequency domain.
The above method might be modified in the following way: instead of multiplying the Fourier Transforms of the image and the mask as a first step, we threshold the Fourier image of the mask to identify the most important frequencies which make up the letter X in the spatial domain. For example, scaling the Fourier magnitude of the above mask to 255 and thresholding it at a value of 10 yields all the frequencies with at least 4% of the peak magnitude, as can be seen in
Now, we multiply this modified mask with the Fourier image of the text, thus retaining only frequencies which also appear in the letter X. Inverse Fourier Transforming this image yields
We can see that the X is the letter which preserved its shape the best and also has higher intensity values. Thresholding this image yields
which correctly identifies the position of the X.
You can interactively experiment with this operator by clicking here.
and compare the results with the images obtained via lowpass filtering.
and then enhance the resulting image using a lowpass filter. Which method would be more suitable and why?
(e.g. a window, the roof or the wall) by creating an appropriate mask and multiplying it with the Fourier Transform of the image.
E. Davies Machine Vision: Theory, Algorithms and Practicalities, Academic Press, 1990, Chap. 9.
R. Gonzalez and R. Woods Digital Image Processing, Addison-Wesley Publishing Company, 1992, Chap. 4.
R. Hamming Digital Filters, Prentice-Hall, 1983.
B. Horn Robot Vision, MIT Press, 1986, Chap. 6.
IEEE Trans. Circuits and Systems Special Issue on Digital Filtering and Image Processing, Vol. CAS-2, 1975.
A. Jain Fundamentals of Digital Image Processing, Prentice-Hall, 1986, Chap. 8.
Specific information about this operator may be found here.
More general advice about the local HIPR installation is available in the Local Information introductory section.
©2003 R. Fisher, S. Perkins,
A. Walker and E. Wolfart.
